【高校数学】 数Ⅱ－８７ 一般角と弧度法 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅱ > 三角関数 > 三角関数とグラフ > 【高校数学】　数Ⅱ－８７　一般角と弧度法

【高校数学】　数Ⅱ－８７　一般角と弧度法

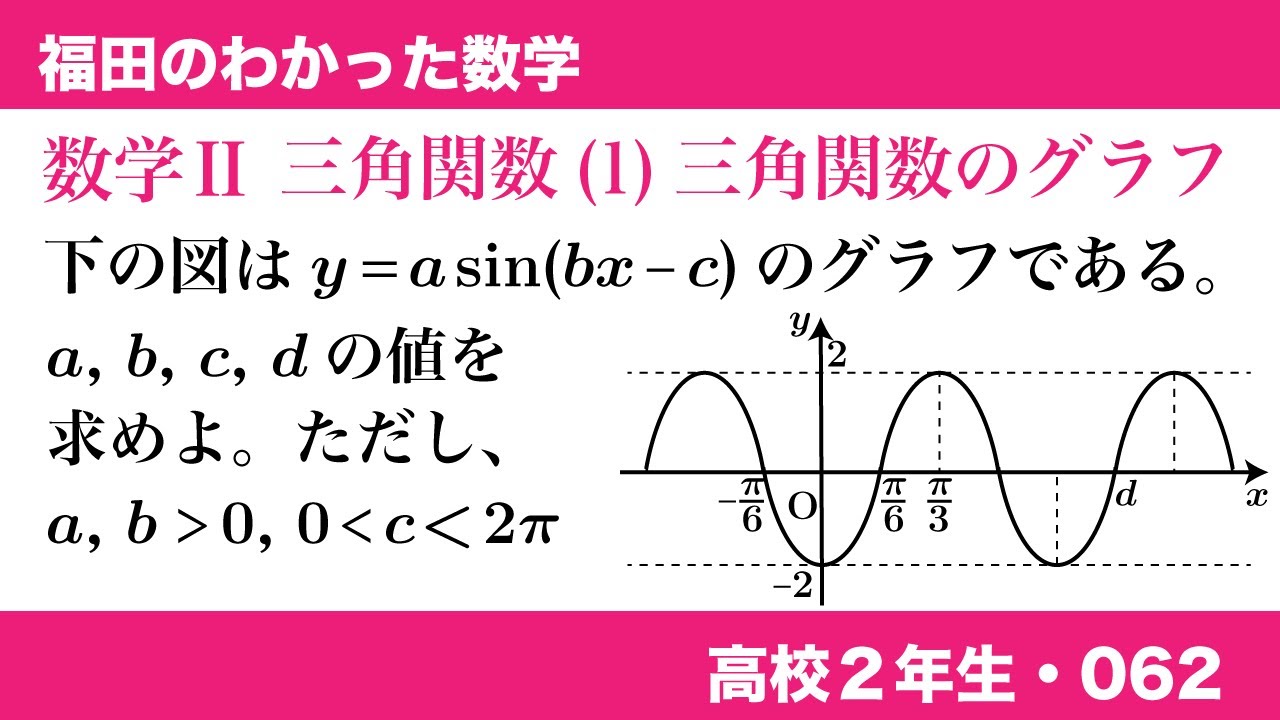
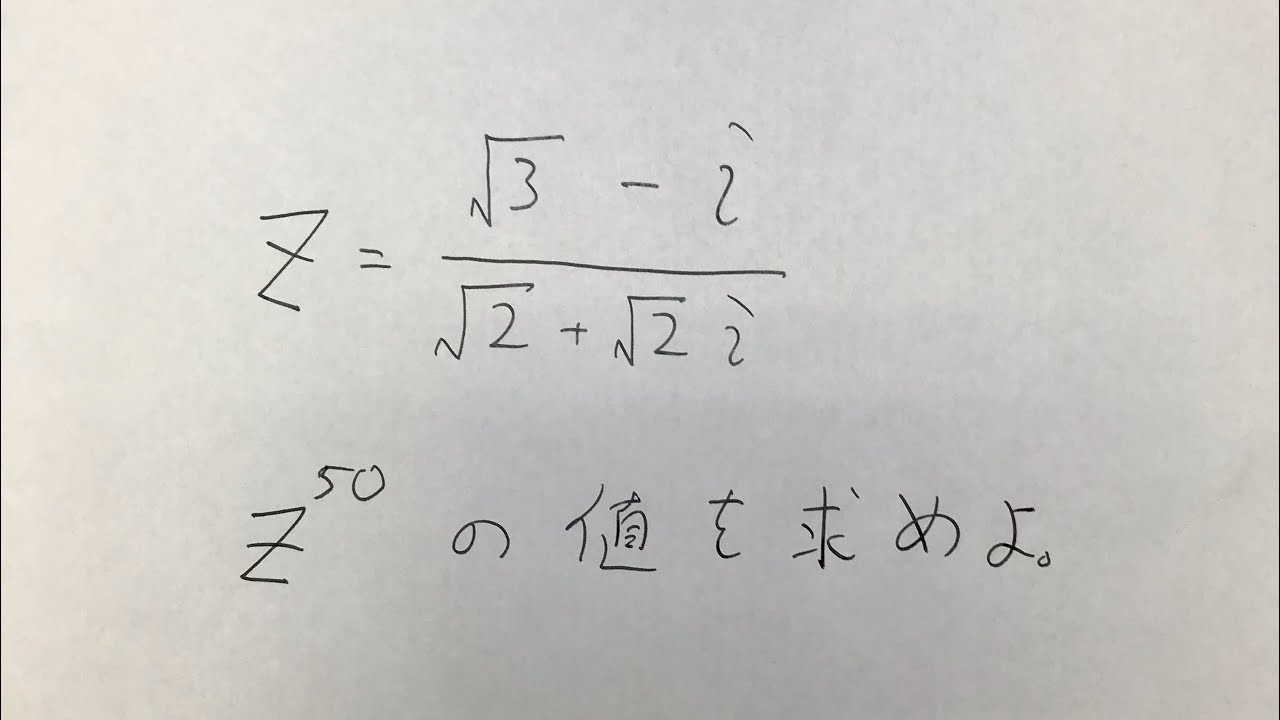問題文全文(内容文)：
◎次の角の憧憬を図示しよう。

①70°

②-150°

③400°

④-635°

◎次の角を、度数は弧度に、弧度は度数に直そう。

⑤30°

⑥135°

⑦210°

⑧$\displaystyle \frac{π}{3}$

⑨$\displaystyle \frac{2}{15}π$

⑩$π$
単元： #数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎次の角の憧憬を図示しよう。

①70°

②-150°

③400°

④-635°

◎次の角を、度数は弧度に、弧度は度数に直そう。

⑤30°

⑥135°

⑦210°

⑧$\displaystyle \frac{π}{3}$

⑨$\displaystyle \frac{2}{15}π$

⑩$π$
投稿日：2015.07.25

＜関連動画＞

15東京都教員採用試験（数学：3番　積分）

アイキャッチ画像
単元： #数Ⅱ#三角関数#三角関数とグラフ#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
3⃣$C_1:y=sin2x,C_2:y=k sinx$
$0 \leqq x \leqq \frac{\pi}{2}$ , $0 < k <2$
(1)$C_1$とx軸で囲まれた図形の面積
(2)$C_1$と$C_2$の原点以外の支点のx座標をαとする。cosαを求めよ。
(3)$C_1$とx軸で囲まれた部分の面積を$C_2$が2等分するときkの値を求めよ。
この動画を見る　

京都大　三角関数　３次関数　解の個数 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$0 \leqq \theta \lt 2\pi$
$\cos 3\theta - \cos 2\theta+3\cos\theta-1=a$を満たす$\theta$の個数

出典：京都大学　過去問
この動画を見る　

30度　45度　60度の直線の式　 A 慶應義塾　2021

アイキャッチ画像
単元： #数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
A,B,Cの座標をaを用いて表せ
＊図は動画内参照

2021慶應義塾高等学校
この動画を見る　

京都大学　５倍角の公式

アイキャッチ画像
単元： #数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）#数Ⅱ#三角関数#三角関数とグラフ
指導講師： 鈴木貫太郎
問題文全文(内容文)：
(1)$\cos5\theta=f(\cos\theta)$を満たす多項式$f(n)$を求めよ.
(2)$\cos\dfrac{\pi}{10}\cos\dfrac{3\pi}{10}\cos\dfrac{7\pi}{10}\cos\dfrac{9\pi}{10}=\dfrac{5}{16}$を示せ.

1996京都大過去問
この動画を見る　

千葉県（改）　令和4年度　数学　関数　2022 入試問題100題解説73問目！！

アイキャッチ画像
単元： #数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
長方形ACDBと長方形CEBFは合同
直線EFの式は？
＊図は動画内参照

2022千葉県
この動画を見る　
Back to top