問題文全文(内容文)：
$\sin\alpha-\sin\beta=\displaystyle \frac{1}{3}$
$\cos\alpha+\cos\beta=\displaystyle \frac{1}{5}$
のとき、$\cos(\alpha+\beta)$の値を求めよ。

出典：2024年東海大学医学部

問題文全文(内容文)：
$0\leqq θ\lt 2π$のとき，次の不等式を解け。
(1) $\sin (θ+\displaystyle \frac{π}{4})\leqq \displaystyle \frac{\sqrt{3}}{2}$

(2) $\tan (θ-\displaystyle \frac{π}{6})\gt 1$

(3) $\cos (θ-\displaystyle \frac{π}{3})\lt -\displaystyle \frac{\sqrt{3}}{2}$

(4) $\tan (θ+\displaystyle \frac{π}{6})\geqq -\sqrt{3}$

問題文全文(内容文)：
三角関数の性質のコツを解説していきます.

問題文全文(内容文)：
$r \sin(\theta+\alpha)$の形に表せ。
ただし、$r>0,-\pi<\alpha≦\pi$とする。
①$\sin\theta-\cos\theta$
②$\frac{\sqrt{3}}{2}\sin\theta+\frac{1}{2}\cos\theta$

問題文全文(内容文)：
共通テスト数学90％取る勉強法説明動画です

問題文全文(内容文)：
数学が共通テストのみの人の勉強法紹介動画です

問題文全文(内容文)：
$0\leqq x\leqq \require{physics}\flatfrac{\pi}{2}$のとき、次の関数が最大となる$x$の値を求めよ。
$y=\sin ^22x+2\cos^2x$

2023中央大学経済学部過去問

問題文全文(内容文)：
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき、次の不等式を解け。
$2\cos^2\theta-\cos\theta \lt 0$

問題文全文(内容文)：
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき、次の等式を満たす$\theta$を求めよ。
$2\sin^2\theta-3\cos\theta=0$

問題文全文(内容文)：
次の角を弧度法で表せ。
（1）
$30^{ \circ }$

（2）
$45^{ \circ }$

（3）
$120^{ \circ }$

（4）
$-90^{ \circ }$

（5）
$108^{ \circ }$

（6）
$390^{ \circ }$

（7）
$\displaystyle \frac{\pi}{3}$

（8）
$\displaystyle \frac{7}{6}\pi$

（9）
$\displaystyle \frac{9}{4}\pi$

（10）
$-\displaystyle \frac{5}{12}n$

（11）
$\displaystyle \frac{11}{2}\pi$

（12）
$3$

問題文全文(内容文)：
2022年度第2回全統記述高2模試全問解説動画です！

問題文全文(内容文)：
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。

2023東北大学理系過去問

問題文全文(内容文)：
三角関数のグラフの説明動画です

問題文全文(内容文)：
a,bを実数とする。θについての方程式

$\cos 2θ =a\sin θ +b$

が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ

2023大阪大学文系過去問

問題文全文(内容文)：
(1)$\cos2\theta,\cos3\theta$を$\cos\theta$を用いて表せ.
(2)半径1の円に内接する正五角形の一辺の長さと1.15の大小比較せよ.

2023京都大過去問

問題文全文(内容文)：
$\Large\boxed{4}$　三角形ABCの内接円の半径をr,　外接円の半径をRとし、h=$\frac{r}{R}$とする。
また、$\angle$A=2α,　$\angle$B=2β,　$\angle$C=2γ とおく。
(1)h=4$\sin\alpha\sin\beta\sin\gamma$となることを示せ。
(2)三角形ABCが直角三角形のときh≦$\sqrt 2-1$が成り立つことを示せ。
また、等号が成り立つのはどのような場合か。
(3)一般の三角形ABCに対してh≦$\frac{1}{2}$が成り立つことを示せ。また等号が成り立つのはどのような場合か。

2018東北大学理系過去問

問題文全文(内容文)：
$\Large\boxed{3}$　αは0＜α≦$\frac{\pi}{2}$を満たす定数とし、四角形ABCDに関する次の2つの条件を考える。
(i)四角形ABCDは半径1の円に内接する。
(ii)$\angle$ABC=$\angle$DAB=α
条件(i)(ii)を満たす四角形のなかで、4辺の長さの積
k=AB・BC・CD・DA
が最大となるものについて、kの値を求めよ。

2018京都大学理系過去問

問題文全文(内容文)：
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa ＞0,b ＞0, a +b＜$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0＜a＜$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。

2020中央大学理工学部過去問

問題文全文(内容文)：
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪＜　①=　②＞
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$＞0が成り立つことは
「$\sin x$＞0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$＜0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }},　\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$＞$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$,　$\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0　①x　②2x　③3x
④4x　⑤5x　⑥6x　⑦$\frac{x}{2}$　
⑧$\frac{3}{2}x$　⑨$\frac{5}{2}x$　ⓐ$\frac{7}{2}x$　ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$,　$\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$,　$a \ne 1$,　$b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$　①$x^b=a$　②$a^x=b$
③$b^x=a$　④$a^b=x$　⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$,　$\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$＞0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数　①bが偶数　②aが奇数　
③bが奇数　④aとbがともに偶数、またはaとbがともに奇数　⑤aとbのいずれか一方が偶数で、もう一方が奇数

2023共通テスト過去問

問題文全文(内容文)：
x,yを実数とする.
$x^2+2y^2+4y=0$を満たすとき,$2x-y$の最大値・最小値を求めよ.

東京電機大過去問

問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}}　(1)\alpha,\betaを実数とする。\\
2\cos\alpha\sin\beta+3\sin\alpha\sin\beta+4\cos\beta\\
の最小値は\boxed{\ \ ア\ \ }である。
\end{eqnarray}

2019早稲田大学商学部過去問

問題文全文(内容文)：
$ \pi<3.3$を示せ.

2022浜松医科大過去問

問題文全文(内容文)：
東大医学部のベテランちさんが、TAWASHIさんに早稲田大学の数学入試を解説します。

問題の解き方を理解しましょう！

問題文全文(内容文)：
三角関数のグラフの移動と拡大について解説します。

問題文全文(内容文)：
（1）
$0^{ \circ } \lt \theta \lt 180^{ \circ }$
$\tan \theta =-2$
$\sin \theta,\cos \theta$は？

（2）
$0 \leqq \theta \lt 2 \pi$
$\cos \theta \lt \displaystyle \frac{\sqrt{ 3 }}{2}$を解け

（3）
$0 \lt \theta \leqq 2 \pi$
$\sin \theta \geqq \displaystyle \frac{1}{2}$を解け

（4）
$0 \leqq \theta \lt 2 \pi$
$\sin \theta + \sqrt{ 3 } \cos \theta =\sqrt{ 2 }$を解け

（5）
$0 \leqq x \leqq \pi$とする
$y=2 \sin 2x-2(\sin x- \cos x)+1$
のとり得る値の範囲は？

（6）
$f(x)=\sin x - \cos 2x$の
$0 \leqq x \leqq \pi$における
max、minを求めよ

問題文全文(内容文)：
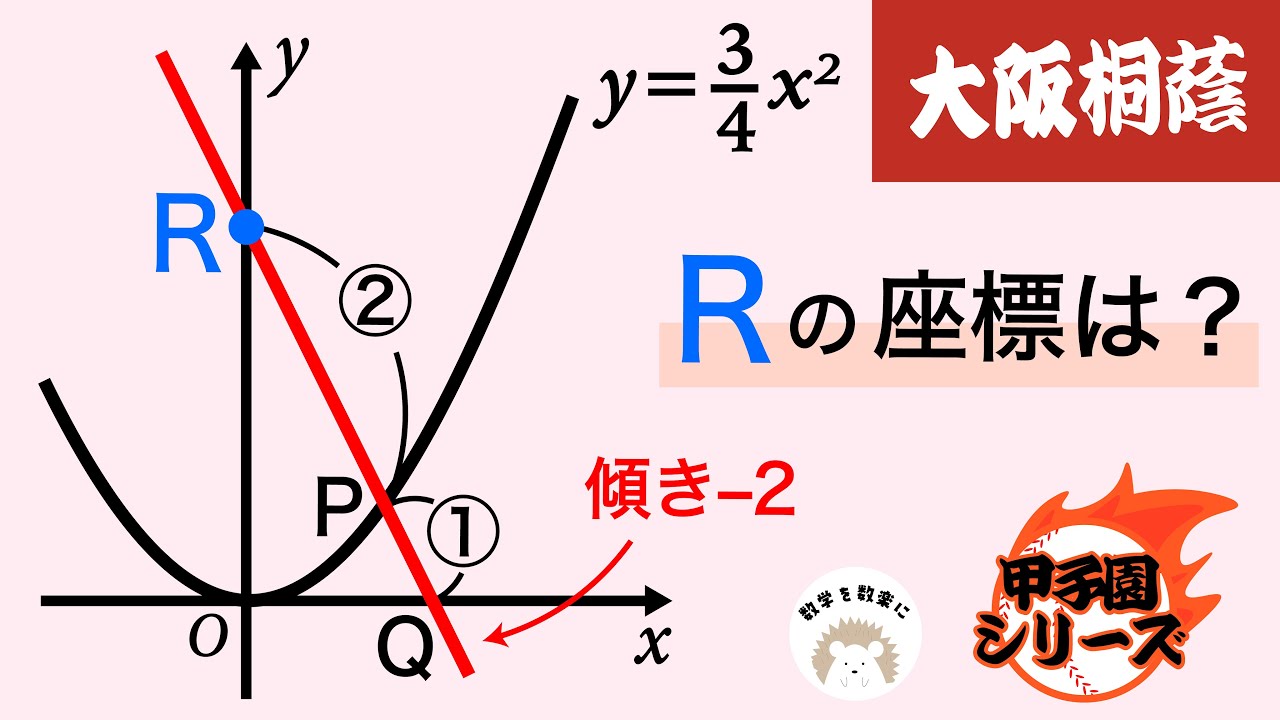
Rの座標は？
＊図は動画内参照

大阪桐蔭高等学校

問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}}\ (2)xを変数とする2次方程式\ x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0\ が\\
異なる2つの実数解をもつような実数\thetaの範囲は\boxed{\ \ ア\ \ }\ である。
\end{eqnarray}

2022慶應義塾大学商学部過去問

問題文全文(内容文)：
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$

問題文全文(内容文)：
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$

問題文全文(内容文)：
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$