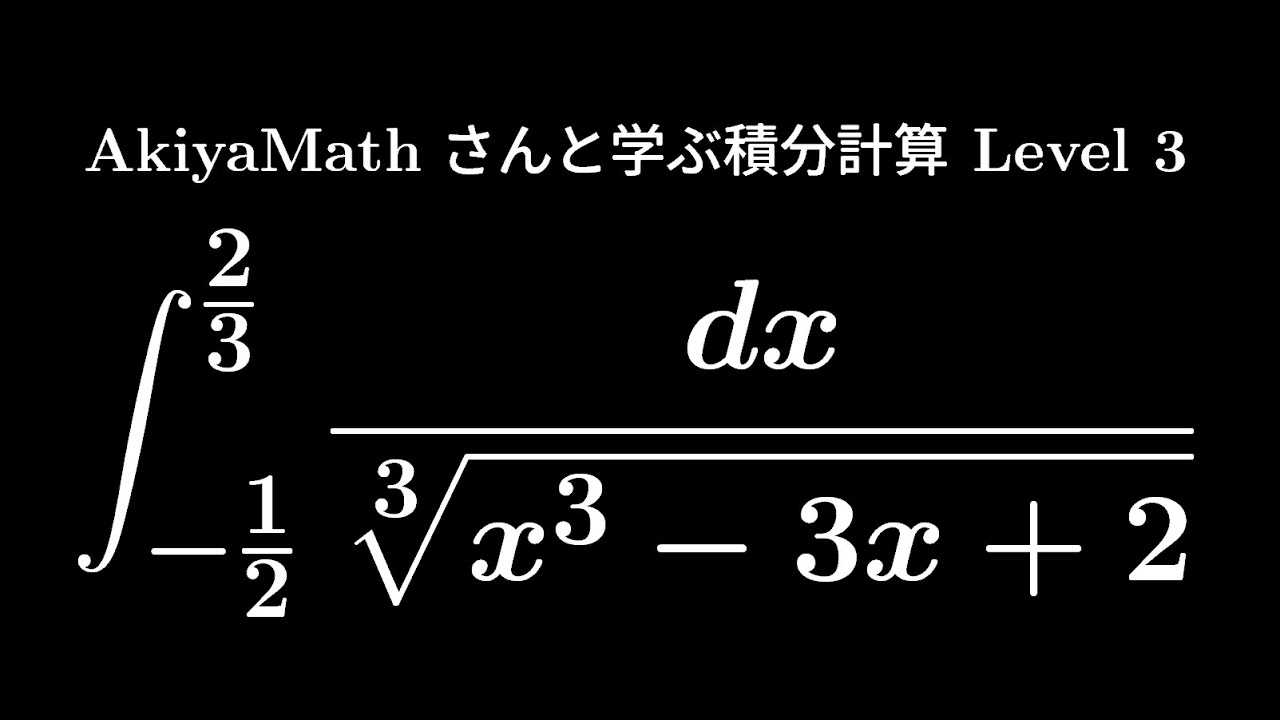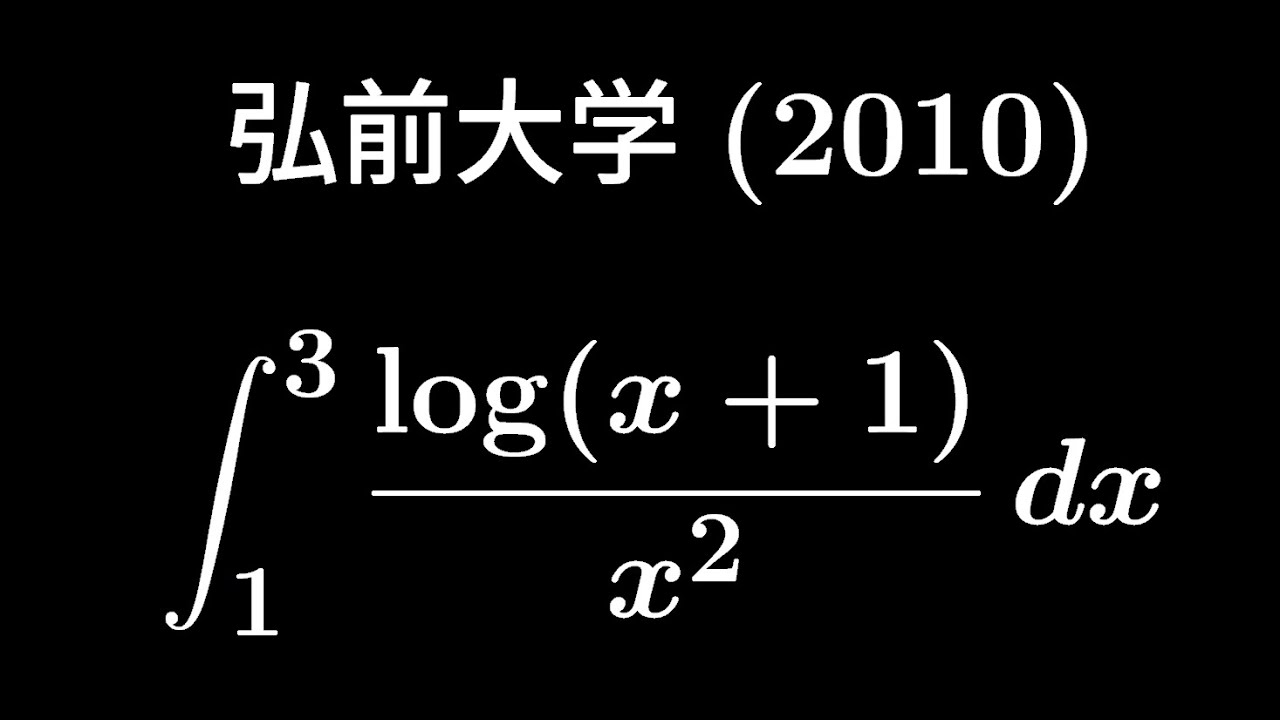問題文全文(内容文):
(1)
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
(2)
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典:2010年横浜国立大学 入試問題
(1)
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
(2)
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典:2010年横浜国立大学 入試問題
チャプター:
00:00 問題紹介
00:25 本編スタート
09:32 作成した解答①
09:43 作成した解答②
09:54 作成した解答③
10:05 エンディング(楽曲提供:兄いえぃさん)
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
(2)
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典:2010年横浜国立大学 入試問題
(1)
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
(2)
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典:2010年横浜国立大学 入試問題
投稿日:2022.11.04