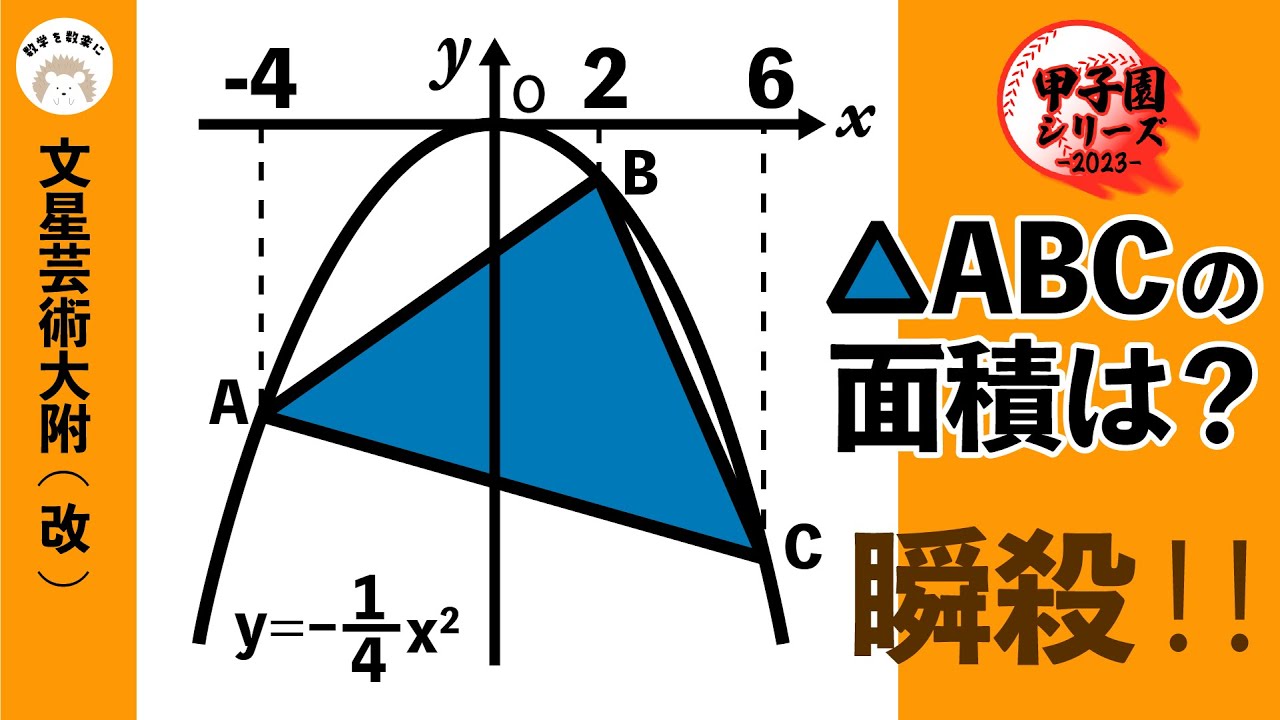
問題文全文(内容文):
$x,y,a,b$は実数とする。
次の[ア]~[ク]に当てはまるものを下の⓪~③の中から選べ。
ただし、同じものを繰り返しで選んでもよい。
(1)$x=2$は、$x^2-x-2=0$であるための[ア]。
(2)$\triangle ABC \sim \triangle PQR$であるための[イ]
(3)$ab+1=a+b$は、$a=1$または$b=1$であるための[ウ]
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(6)$|a| \lt 1$かつ$|b| \lt 1$は、$ab+1 \gt a+b$であるための[カ]
(7)$xy(y-1)=0$であることは$x=y(y-1)=0$であるための[キ]
(8)$x^2y^2+(y-1)^2=0$であることは$x=y(y-1=0)$であるための[ク]
$x,y,a,b$は実数とする。
次の[ア]~[ク]に当てはまるものを下の⓪~③の中から選べ。
ただし、同じものを繰り返しで選んでもよい。
(1)$x=2$は、$x^2-x-2=0$であるための[ア]。
(2)$\triangle ABC \sim \triangle PQR$であるための[イ]
(3)$ab+1=a+b$は、$a=1$または$b=1$であるための[ウ]
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(6)$|a| \lt 1$かつ$|b| \lt 1$は、$ab+1 \gt a+b$であるための[カ]
(7)$xy(y-1)=0$であることは$x=y(y-1)=0$であるための[キ]
(8)$x^2y^2+(y-1)^2=0$であることは$x=y(y-1=0)$であるための[ク]
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$x,y,a,b$は実数とする。
次の[ア]~[ク]に当てはまるものを下の⓪~③の中から選べ。
ただし、同じものを繰り返しで選んでもよい。
(1)$x=2$は、$x^2-x-2=0$であるための[ア]。
(2)$\triangle ABC \sim \triangle PQR$であるための[イ]
(3)$ab+1=a+b$は、$a=1$または$b=1$であるための[ウ]
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(6)$|a| \lt 1$かつ$|b| \lt 1$は、$ab+1 \gt a+b$であるための[カ]
(7)$xy(y-1)=0$であることは$x=y(y-1)=0$であるための[キ]
(8)$x^2y^2+(y-1)^2=0$であることは$x=y(y-1=0)$であるための[ク]
$x,y,a,b$は実数とする。
次の[ア]~[ク]に当てはまるものを下の⓪~③の中から選べ。
ただし、同じものを繰り返しで選んでもよい。
(1)$x=2$は、$x^2-x-2=0$であるための[ア]。
(2)$\triangle ABC \sim \triangle PQR$であるための[イ]
(3)$ab+1=a+b$は、$a=1$または$b=1$であるための[ウ]
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(6)$|a| \lt 1$かつ$|b| \lt 1$は、$ab+1 \gt a+b$であるための[カ]
(7)$xy(y-1)=0$であることは$x=y(y-1)=0$であるための[キ]
(8)$x^2y^2+(y-1)^2=0$であることは$x=y(y-1=0)$であるための[ク]
投稿日:2020.11.01