集合と命題（集合・命題と条件・背理法）
集合と命題（集合・命題と条件・背理法）
無理数の無理数乗が有理数
数と式 4STEP数Ⅰ 119,120 証明の応用【いつものシミズ君がていねいに解説】
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#4STEP(4ステップ）数学#4STEP数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たす有理数ｐ、ｑの値を求めよ。
（１）$（\sqrt{2}-1）p＋q\sqrt{2}＝2+\sqrt{2}$
（２）$\dfrac{p}{\sqrt{2}-1}+\dfrac{q}{\sqrt{2}}=1$
ｐ、ｑは有理数、Xが無理数でｐ+qX=0であるならば
p=q=0であることを証明せよ
この動画を見る
次の条件を満たす有理数ｐ、ｑの値を求めよ。
（１）$（\sqrt{2}-1）p＋q\sqrt{2}＝2+\sqrt{2}$
（２）$\dfrac{p}{\sqrt{2}-1}+\dfrac{q}{\sqrt{2}}=1$
ｐ、ｑは有理数、Xが無理数でｐ+qX=0であるならば
p=q=0であることを証明せよ
数と式 4STEP数Ⅰ 117,118 対偶の使うタイミング【いつものシミズ君がていねいに解説】
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#4STEP(4ステップ）数学#4STEP数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【1問目】
ｍ、nは整数とする。次の命題を証明せよ。
（１）n²が5の倍数ならば、nは５の倍数である。
（２）mnが３の倍数ならば、m,nの少なくとも一方は３の倍数である。
【2問目】
√6が無理数であることを用いて、√3－√2は無理数であることを証明せよ。
この動画を見る
【1問目】
ｍ、nは整数とする。次の命題を証明せよ。
（１）n²が5の倍数ならば、nは５の倍数である。
（２）mnが３の倍数ならば、m,nの少なくとも一方は３の倍数である。
【2問目】
√6が無理数であることを用いて、√3－√2は無理数であることを証明せよ。
数と式 4STEP数Ⅰ 110,111 背理法の使うタイミング【いつものシミズ君がていねいに解説】
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#4STEP(4ステップ）数学#4STEP数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式
指導講師：
理数個別チャンネル
問題文全文(内容文)：
ｘ、ｙ、zは実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
【110】
（１） （ｘ－ｙ）（ｙ－ｚ）＝０はｘ＝ｙ＝ｚであるための▢
（２） 「ｘ＞０ かつ ｙ＞０」は、ｘｙ＞0であるための▢
（３） ｘ＝ｙ＝０は、「ｘｙ＝０かつｘ＋ｙ＝０」であるための▢
（４） ∠Ａ＜90は△ＡＢＣが鋭角三角形であるための▢
（５） △ＡＢＣの3辺ＢＣ，ＣＡ，ＡＢの長さがそれぞれa,b,cとする。
（a-b）(a²+b²＝ｃ²）＝０は△ＡＢＣが直角二等辺三角形であるための▢
【111】
a,bは実数とする。次の2つの条件ｐ、ｑは同値であることを証明せよ。
p:a＞１かつb＞１ q:a+b＞２かつ(a-1)(b-1)＞０
この動画を見る
ｘ、ｙ、zは実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
【110】
（１） （ｘ－ｙ）（ｙ－ｚ）＝０はｘ＝ｙ＝ｚであるための▢
（２） 「ｘ＞０ かつ ｙ＞０」は、ｘｙ＞0であるための▢
（３） ｘ＝ｙ＝０は、「ｘｙ＝０かつｘ＋ｙ＝０」であるための▢
（４） ∠Ａ＜90は△ＡＢＣが鋭角三角形であるための▢
（５） △ＡＢＣの3辺ＢＣ，ＣＡ，ＡＢの長さがそれぞれa,b,cとする。
（a-b）(a²+b²＝ｃ²）＝０は△ＡＢＣが直角二等辺三角形であるための▢
【111】
a,bは実数とする。次の2つの条件ｐ、ｑは同値であることを証明せよ。
p:a＞１かつb＞１ q:a+b＞２かつ(a-1)(b-1)＞０
【いつものシミズ君がていねいに解説】数と式 4STEP数Ⅰ 108,109 真偽の調べ方
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#4STEP(4ステップ）数学#4STEP数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式
指導講師：
理数個別チャンネル
問題文全文(内容文)：
動画について不明点や質問などあればコメント欄にお気軽にお書きください！
質問解決D.B.（データベース） - 算数・数学・英語・理科等の問題別・単元別の解説動画のまとめサイトです。
https://kaiketsu-db.net/
■問題文
a,bは実数とする。次の命題の真偽を求めよ。
（１）ab=0ならばa²+b²=0である。
（２）a²=4ならば|a+1|≧1である。
（３）abが有理数であるならば、a、bはともに有理数である。
（４）a+b、abがともに有理数ならば、a、bはともに有理数である。
全体集合をUとし、条件p、qを満たす全体の集合を、それぞれＰ．Ｑとする。
命題p（補集合）⇒qが真であるとき、P、Qについて常に成り立つ事をすべて選べ。
①P＝Q
②Q⊂P
③Q（補集合）⊂P
④P⊂Q（補集合）
⑤P∪Q（補集合）＝P
⑥P∪Q（補集合）＝Q（補集合）
⑦P∩Q＝∅
⑧P∪Q＝U
この動画を見る
動画について不明点や質問などあればコメント欄にお気軽にお書きください！
質問解決D.B.（データベース） - 算数・数学・英語・理科等の問題別・単元別の解説動画のまとめサイトです。
https://kaiketsu-db.net/
■問題文
a,bは実数とする。次の命題の真偽を求めよ。
（１）ab=0ならばa²+b²=0である。
（２）a²=4ならば|a+1|≧1である。
（３）abが有理数であるならば、a、bはともに有理数である。
（４）a+b、abがともに有理数ならば、a、bはともに有理数である。
全体集合をUとし、条件p、qを満たす全体の集合を、それぞれＰ．Ｑとする。
命題p（補集合）⇒qが真であるとき、P、Qについて常に成り立つ事をすべて選べ。
①P＝Q
②Q⊂P
③Q（補集合）⊂P
④P⊂Q（補集合）
⑤P∪Q（補集合）＝P
⑥P∪Q（補集合）＝Q（補集合）
⑦P∩Q＝∅
⑧P∪Q＝U
【いつものシミズ君がていねいに解説】数と式 4STEP数Ⅰ 98,99,100 集合の考え方
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#4STEP(4ステップ）数学#4STEP数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式
指導講師：
理数個別チャンネル
問題文全文(内容文)：
U＝｛1,2,3,4,5,6,7,8,9｝を全体集合とする。Uの部分集合A、Bについて
A∩B＝｛2｝ A（補集合）∩B＝｛4,6,8｝ A（補集合）∩B（補集合）＝｛1.9｝
であるとき、次の∩を求めよ。
（１）A∪B
（２）B
（３）A∩B（補集合）
U＝{x|1≦x≦10、xは整数}を全体集合とする。Uの部分集合
A＝｛1,2,3,4,8｝B＝｛3,4,5,6｝C｛2,3,6,7｝
について、次の集合を求めよ。
（１）A∩B∩C
（２）A∪B∪C
（３）A∩B∩C（補集合）
（４）A（補集合）∩B∩C（補集合）
（５）（A∩B∩C）（補集合）
（６）（A∪C）∩B（補集合）
A＝{1、3、3a-2} B＝{－5、a+2、a²-2a+1} A∩B＝｛1、４｝のとき
定数aの値と和集合A∪Bを求めよ。
この動画を見る
U＝｛1,2,3,4,5,6,7,8,9｝を全体集合とする。Uの部分集合A、Bについて
A∩B＝｛2｝ A（補集合）∩B＝｛4,6,8｝ A（補集合）∩B（補集合）＝｛1.9｝
であるとき、次の∩を求めよ。
（１）A∪B
（２）B
（３）A∩B（補集合）
U＝{x|1≦x≦10、xは整数}を全体集合とする。Uの部分集合
A＝｛1,2,3,4,8｝B＝｛3,4,5,6｝C｛2,3,6,7｝
について、次の集合を求めよ。
（１）A∩B∩C
（２）A∪B∪C
（３）A∩B∩C（補集合）
（４）A（補集合）∩B∩C（補集合）
（５）（A∩B∩C）（補集合）
（６）（A∪C）∩B（補集合）
A＝{1、3、3a-2} B＝{－5、a+2、a²-2a+1} A∩B＝｛1、４｝のとき
定数aの値と和集合A∪Bを求めよ。
【さこすけ’s サイエンスがていねいに解説】場合の数 4STEP数A 9,10,11 集合の基本～ベン図を描こう～
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#4STEP(4ステップ）数学#4STEP数学Ⅰ＋AのB問題解説（新課程2022年以降）#集合と命題
指導講師：
理数個別チャンネル
問題文全文(内容文)：
U＝｛1,2,3,4,5,6,7,8,9｝を全体集合とする。Uの部分集合A,Bについて、
A∩B＝｛2｝,(Aの補集合)∩B＝｛2,4,6,8｝,(Aの補集合)∩(Bの補集合)＝｛1,9｝であるとき、次の集合を求めよ。
(1)A∪B (2)B (3)A∩(Bの補集合)
U＝｛x|1≦x≦10,xは整数｝を全体集合とする。Uの部分集合
A＝｛1,2,3,4,8｝,B＝｛3,4,5,6｝,C＝｛2,3,6,7｝について、次の集合を求めよ。
(1)A∩B∩C (2)A∪B∪C (3)A∩B∩(Cの補集合) (4)(Aの補集合)∩B∩(Cの補集合) (5)(A∩B∩Cの補集合) (6)(A∪C)∩(Bの補集合)
A＝｛1,3,3a-2｝,B＝｛-5,a+2,a²-2a+1｝,A∩B＝｛1,4｝のとき、
定数aの値と和集合A∪Bを求めよ
この動画を見る
U＝｛1,2,3,4,5,6,7,8,9｝を全体集合とする。Uの部分集合A,Bについて、
A∩B＝｛2｝,(Aの補集合)∩B＝｛2,4,6,8｝,(Aの補集合)∩(Bの補集合)＝｛1,9｝であるとき、次の集合を求めよ。
(1)A∪B (2)B (3)A∩(Bの補集合)
U＝｛x|1≦x≦10,xは整数｝を全体集合とする。Uの部分集合
A＝｛1,2,3,4,8｝,B＝｛3,4,5,6｝,C＝｛2,3,6,7｝について、次の集合を求めよ。
(1)A∩B∩C (2)A∪B∪C (3)A∩B∩(Cの補集合) (4)(Aの補集合)∩B∩(Cの補集合) (5)(A∩B∩Cの補集合) (6)(A∪C)∩(Bの補集合)
A＝｛1,3,3a-2｝,B＝｛-5,a+2,a²-2a+1｝,A∩B＝｛1,4｝のとき、
定数aの値と和集合A∪Bを求めよ
福田の数学〜上智大学2022年TEAP理系型第１問(3)〜命題と必要十分な条件
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
1
(3) aを正の実数とする。 実数からなる集合X, Yを次で定める。
X={x|0 < x < a}, Y={y|3 < y < 5}
次のそれぞれの命題が成り立つための必要十分条件を、選択肢から1つずつ選べ。
(i) すべてのx∈Xとすべてのy∈Yに対してx
この動画を見る
1
(3) aを正の実数とする。 実数からなる集合X, Yを次で定める。
X={x|0 < x < a}, Y={y|3 < y < 5}
次のそれぞれの命題が成り立つための必要十分条件を、選択肢から1つずつ選べ。
(i) すべてのx∈Xとすべてのy∈Yに対してx
福田の数学〜慶應義塾大学2022年商学部第１問(1)〜倍数の個数を数える
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}}\ (1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数\\
は\boxed{\ \ アイウ\ \ }\ 個あり、2,3,5の少なくとも1つで割り切れ、\\
かつ6で割り切れない数は\boxed{\ \ エオカ\ \ }\ 個ある。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}}\ (1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数\\
は\boxed{\ \ アイウ\ \ }\ 個あり、2,3,5の少なくとも1つで割り切れ、\\
かつ6で割り切れない数は\boxed{\ \ エオカ\ \ }\ 個ある。
\end{eqnarray}
cos1°は有理数か【数学 入試問題】【チェビシェフ多項式】
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角関数#加法定理とその応用#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
この動画を見る
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
【有名問題】京都大学の伝説の問題です【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$ tan1°$は有理数か？
この動画を見る
$ tan1°$は有理数か？
格子点を通るということは？【山口大学】【数学 入試問題】
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
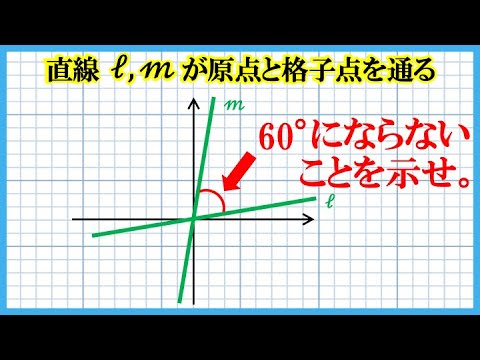
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
この動画を見る
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
整数問題【一橋大学】【数学 入試問題】
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$x$は0でない実数とする。$x-\dfrac{1}{x}$が0以外の整数ならば$x^2-\dfrac{1}{x^2}$は整数でないことを示せ。
この動画を見る
$x$は0でない実数とする。$x-\dfrac{1}{x}$が0以外の整数ならば$x^2-\dfrac{1}{x^2}$は整数でないことを示せ。
【数Ⅰ】体系問題集3(論理・確率編)10：集合と命題：集合：要素の決定
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#体系数学#体系数学問題集3(論理・確率編)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
A=｛2,4,x-1｝,B=｛3,2x-y-1｝,C=｛2,2x+z-2｝とする。
B⊂A、B=Cが成り立つとき、x,y,zの値を求めよう。
この動画を見る
A=｛2,4,x-1｝,B=｛3,2x-y-1｝,C=｛2,2x+z-2｝とする。
B⊂A、B=Cが成り立つとき、x,y,zの値を求めよう。
福田のわかった数学〜高校１年生037〜部屋割り論法(2)の訂正版
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 部屋割り論法(2)\\
座標平面上に異なる5個の格子点がある。これら5個の格子点の中に、\\
結んだ線分の中点がまた格子点となるような2点が存在することを示せ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 部屋割り論法(2)\\
座標平面上に異なる5個の格子点がある。これら5個の格子点の中に、\\
結んだ線分の中点がまた格子点となるような2点が存在することを示せ。
\end{eqnarray}
福田のわかった数学〜高校１年生037〜部屋割り論法(2)
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 部屋割り論法(2)\\
座標平面上で異なる5個の格子点の\\
どれか2個を結ぶと、その中点が格子点になることを証明せよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 部屋割り論法(2)\\
座標平面上で異なる5個の格子点の\\
どれか2個を結ぶと、その中点が格子点になることを証明せよ。
\end{eqnarray}
福田の数学〜慶應義塾大学2021年環境情報学部第４問〜条件を満たす部分集合の個数
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{4}} A_n=\left\{1,2,\ldots,n\right\}を、1からnまでの自然数の集合とする。SをA_nの部分集合\\
(空集合およびA_n自身も含む)としたとき、S'をSの要素それぞれに1を加えてできた\\
集合とする。またS''をS'の要素それぞれにさらに1を加えてできた集合とする。\\
たとえば、A_3=\left\{1,2,3\right\}の部分集合S=\left\{1,3\right\}の場合、S'=\left\{2,4\right\},S''=\left\{3,5\right\}\\
\\
(1)A_4=\left\{1,2,3,4\right\}の部分集合S=\left\{1,2,3\right\}はS \cup S'=A_4となる。このように\\
A_4の部分集合でS \cup S'=A_4となるものは\left\{1,2,3\right\}と\left\{1,\boxed{\ \ ア\ \ }\right\}の2つである。\\
\\
(2)A_nの部分集合SでS \cup S'=A_nとなるようなSの個数をa_nとすると、(1)から\\
分かるようにa_4=2であり\\
a_5=\boxed{\ \ イウ\ \ },a_6=\boxed{\ \ エオ\ \ },a_7=\boxed{\ \ カキ\ \ },a_8=\boxed{\ \ クケ\ \ },\ldots,a_{16}=\boxed{\ \ コサシ\ \ }\\
となる。\\
\\
(3)A_4=\left\{1,2,3,4\right\}の部分集合SでS \cup S''=A_4となるものはS=\left\{1,\boxed{\ \ ス\ \ }\right\}だけ\\
である。\\
\\
(4)A_nの部分集合SでS \cup S''=A_nとなるようなSの個数をb_nとすると、(3)から\\
分かうようにb_4=1であり\\
b_5=\boxed{\ \ セソ\ \ },b_6=\boxed{\ \ タチ\ \ },b_7=\boxed{\ \ ツテ\ \ },b_8=\boxed{\ \ トナ\ \ },\ldots,b_{16}=\boxed{\ \ ニヌネ\ \ }\\
となる。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{4}} A_n=\left\{1,2,\ldots,n\right\}を、1からnまでの自然数の集合とする。SをA_nの部分集合\\
(空集合およびA_n自身も含む)としたとき、S'をSの要素それぞれに1を加えてできた\\
集合とする。またS''をS'の要素それぞれにさらに1を加えてできた集合とする。\\
たとえば、A_3=\left\{1,2,3\right\}の部分集合S=\left\{1,3\right\}の場合、S'=\left\{2,4\right\},S''=\left\{3,5\right\}\\
\\
(1)A_4=\left\{1,2,3,4\right\}の部分集合S=\left\{1,2,3\right\}はS \cup S'=A_4となる。このように\\
A_4の部分集合でS \cup S'=A_4となるものは\left\{1,2,3\right\}と\left\{1,\boxed{\ \ ア\ \ }\right\}の2つである。\\
\\
(2)A_nの部分集合SでS \cup S'=A_nとなるようなSの個数をa_nとすると、(1)から\\
分かるようにa_4=2であり\\
a_5=\boxed{\ \ イウ\ \ },a_6=\boxed{\ \ エオ\ \ },a_7=\boxed{\ \ カキ\ \ },a_8=\boxed{\ \ クケ\ \ },\ldots,a_{16}=\boxed{\ \ コサシ\ \ }\\
となる。\\
\\
(3)A_4=\left\{1,2,3,4\right\}の部分集合SでS \cup S''=A_4となるものはS=\left\{1,\boxed{\ \ ス\ \ }\right\}だけ\\
である。\\
\\
(4)A_nの部分集合SでS \cup S''=A_nとなるようなSの個数をb_nとすると、(3)から\\
分かうようにb_4=1であり\\
b_5=\boxed{\ \ セソ\ \ },b_6=\boxed{\ \ タチ\ \ },b_7=\boxed{\ \ ツテ\ \ },b_8=\boxed{\ \ トナ\ \ },\ldots,b_{16}=\boxed{\ \ ニヌネ\ \ }\\
となる。
\end{eqnarray}
福田のわかった数学〜高校１年生035〜必要条件・十分条件
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 必要条件・十分条件\\
a \gt 0とする。2つの条件p,qを\\
p:|x-1| \leqq a, q:|x| \lt 2 とする。\\
\\
(1)pがqの十分条件となるaの範囲\\
(2)pがqの必要条件となるaの範囲\\
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 必要条件・十分条件\\
a \gt 0とする。2つの条件p,qを\\
p:|x-1| \leqq a, q:|x| \lt 2 とする。\\
\\
(1)pがqの十分条件となるaの範囲\\
(2)pがqの必要条件となるaの範囲\\
\end{eqnarray}
福田の数学〜慶應義塾大学2021年医学部第１問(3)〜集合の要素の個数と2次方程式の解
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#集合と命題（集合・命題と条件・背理法）#複素数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}} (3)整数kに対して、xの2次方程式x^2+kx+k+35=0の解を\alpha_k,\beta_kとおく。\\
ただし、方程式が重解をもつときは\alpha_k=\beta_kである。また\\
U=\left\{k|kは整数、かつ|k| \leqq 100 \right\}\\
を全体集合とし、その部分集合\\
A=\left\{k|k \in Uかつ\alpha_k,\beta_kはともに実数で\alpha_k≠\beta_k\right\}\\
B=\left\{k|k \in Uかつ\alpha_k,\beta_kの実数はともに2より大きい\right\}\\
C=\left\{k|k \in Uかつ\alpha_k,\beta_kの実部と虚部はすべて整数\right\}\\
を考える。このときn(A)=\boxed{\ \ (か)\ \ },n(A \cap B)=\boxed{\ \ (き)\ \ },n(\bar{ A } \cap B)=\boxed{\ \ (く)\ \ },\\
n(A \cap C)=\boxed{\ \ (け)\ \ },n(\bar{ A } \cap C)=\boxed{\ \ (こ)\ \ }である。ただし有限集合Xに対して\\
その要素の個数をn(X)で表す。また\bar{ A }はAの補集合である。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} (3)整数kに対して、xの2次方程式x^2+kx+k+35=0の解を\alpha_k,\beta_kとおく。\\
ただし、方程式が重解をもつときは\alpha_k=\beta_kである。また\\
U=\left\{k|kは整数、かつ|k| \leqq 100 \right\}\\
を全体集合とし、その部分集合\\
A=\left\{k|k \in Uかつ\alpha_k,\beta_kはともに実数で\alpha_k≠\beta_k\right\}\\
B=\left\{k|k \in Uかつ\alpha_k,\beta_kの実数はともに2より大きい\right\}\\
C=\left\{k|k \in Uかつ\alpha_k,\beta_kの実部と虚部はすべて整数\right\}\\
を考える。このときn(A)=\boxed{\ \ (か)\ \ },n(A \cap B)=\boxed{\ \ (き)\ \ },n(\bar{ A } \cap B)=\boxed{\ \ (く)\ \ },\\
n(A \cap C)=\boxed{\ \ (け)\ \ },n(\bar{ A } \cap C)=\boxed{\ \ (こ)\ \ }である。ただし有限集合Xに対して\\
その要素の個数をn(X)で表す。また\bar{ A }はAの補集合である。
\end{eqnarray}
福田のわかった数学〜高校１年生034〜背理法(2)
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 背理法(2)\\
\sqrt2,\sqrt[3]3が無理数であることを既知として次を証明せよ。\\
p,q,\sqrt2p+\sqrt[3]3qが全て有理数 \Rightarrow p=q=0
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 背理法(2)\\
\sqrt2,\sqrt[3]3が無理数であることを既知として次を証明せよ。\\
p,q,\sqrt2p+\sqrt[3]3qが全て有理数 \Rightarrow p=q=0
\end{eqnarray}
福田のわかった数学〜高校１年生033〜背理法(1)
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 背理法(1)\\
\sqrt2,\ \sqrt[3]3 が無理数であることを証明せよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 背理法(1)\\
\sqrt2,\ \sqrt[3]3 が無理数であることを証明せよ。
\end{eqnarray}
福田のわかった数学〜高校１年生032〜否定分の作り方(2)
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 否定分の作り方(2)\\
次の関数f(x)についての命題を否定せよ。\\
\\
「N以上の全ての自然数nについてf(n) \leqq 2」\\
が成り立つような自然数Nが存在する。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 否定分の作り方(2)\\
次の関数f(x)についての命題を否定せよ。\\
\\
「N以上の全ての自然数nについてf(n) \leqq 2」\\
が成り立つような自然数Nが存在する。
\end{eqnarray}
福田のわかった数学〜高校１年生031〜否定分の作り方(1)
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} 否定分の作り方(1)\\
次の命題を否定せよ。\\
砂糖は甘い。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 否定分の作り方(1)\\
次の命題を否定せよ。\\
砂糖は甘い。
\end{eqnarray}
【数Ⅰ】集合と命題：センター試験2013年
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
三角形に関する条件p,q,rを次のように定める。p:3つの内角がすべて異なる q:直角三角形でない r:45度の内角は1つもない。条件pの否定をpバーで表し、同様にq,rはそれぞれ条件qバー、rバーの否定を表すものとする。
[1]命題｢r ⇒ (pまたはq)｣の対偶は｢(ア)⇒r｣である。(ア)に当てはまるものを, 次の(0)～(3)のうちから1つ選べ。
(0)(pかつq) (1) (pかつq) (2) (pまたはq ) (3) (pまたはq)
[2] 次の(0)～(4)のうち、命題｢(pまたはq) ⇒ r｣に対する反例となっている三角形は(イ)と(ウ)である。(イ)と(ウ)に当てはまるものを、(0)～(4)のうちから1つずつ選べ。ただし、(イ)と(ウ)の解答の順序は問わない。
(0) 直角二等辺三角形 (1) 内角が30度,45度,105度の三角形 (2) 正三角形 (3) 3辺の長さが3,4,5の三角形 (4) 頂角が45度の二等辺三角形
[3] rは(pまたはq)であるための(エ) 。(エ)に当てはまるものを、次の(0)～(3)のうちから1つ選べ。
(0) 必要十分条件である (1) 必要条件であるが十分条件ではない (2) 十分条件であるが必要条件ではない (3) 必要条件でも十分条件でもない
この動画を見る
三角形に関する条件p,q,rを次のように定める。p:3つの内角がすべて異なる q:直角三角形でない r:45度の内角は1つもない。条件pの否定をpバーで表し、同様にq,rはそれぞれ条件qバー、rバーの否定を表すものとする。
[1]命題｢r ⇒ (pまたはq)｣の対偶は｢(ア)⇒r｣である。(ア)に当てはまるものを, 次の(0)～(3)のうちから1つ選べ。
(0)(pかつq) (1) (pかつq) (2) (pまたはq ) (3) (pまたはq)
[2] 次の(0)～(4)のうち、命題｢(pまたはq) ⇒ r｣に対する反例となっている三角形は(イ)と(ウ)である。(イ)と(ウ)に当てはまるものを、(0)～(4)のうちから1つずつ選べ。ただし、(イ)と(ウ)の解答の順序は問わない。
(0) 直角二等辺三角形 (1) 内角が30度,45度,105度の三角形 (2) 正三角形 (3) 3辺の長さが3,4,5の三角形 (4) 頂角が45度の二等辺三角形
[3] rは(pまたはq)であるための(エ) 。(エ)に当てはまるものを、次の(0)～(3)のうちから1つ選べ。
(0) 必要十分条件である (1) 必要条件であるが十分条件ではない (2) 十分条件であるが必要条件ではない (3) 必要条件でも十分条件でもない
【数I】集合と命題：条件の否定：否定は○○“じゃない”
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
かつ、または、すべて(任意)、あるの否定。
文字はすべて実数とする。次の条件の否定を述べよ。
(1)x>0かつy≦0
(2)x≧2またはx<-3
(3)a=b=c=0
この動画を見る
かつ、または、すべて(任意)、あるの否定。
文字はすべて実数とする。次の条件の否定を述べよ。
(1)x>0かつy≦0
(2)x≧2またはx<-3
(3)a=b=c=0
【数Ⅰ】集合と命題：実数全体を全体集合とし、その部分集合A, B, CをA={x| -3≦x≦5}, B={x| |x|<4}, C={x| k-7≦x≦k+3} (kは定数)とする。
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
実数全体を全体集合とし、その部分集合A, B, CをA={x| -3≦x≦5}, B={x| |x|<4}, C={x| k-7≦x≦k+3} (kは定数)とする。
(1)次の集合を求めよう。
(ア)Bバー
(イ)A∪Bバー
(ウ)A∩Bバー。
(2)A⊂Cとなるkの値の範囲を求めよう。
この動画を見る
実数全体を全体集合とし、その部分集合A, B, CをA={x| -3≦x≦5}, B={x| |x|<4}, C={x| k-7≦x≦k+3} (kは定数)とする。
(1)次の集合を求めよう。
(ア)Bバー
(イ)A∪Bバー
(ウ)A∩Bバー。
(2)A⊂Cとなるkの値の範囲を求めよう。
【数Ⅰ】集合と命題：実数aに対して2つの集合をA=｛a-1, 4, a²-5a+6｝,B=｛1, a²-4, a²-7a+12, 4｝とする。A∩B=｛0, 4｝であるとき、aの値を求めよう。
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
実数aに対して2つの集合をA=｛a-1, 4, a²-5a+6｝,B=｛1, a²-4, a²-7a+12, 4｝とする。A∩B=｛0, 4｝であるとき、aの値を求めよう。
この動画を見る
実数aに対して2つの集合をA=｛a-1, 4, a²-5a+6｝,B=｛1, a²-4, a²-7a+12, 4｝とする。A∩B=｛0, 4｝であるとき、aの値を求めよう。
【数Ⅰ】体系問題集3(論理・確率編)33：集合と命題：命題と証明：背理法を使った証明
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#体系数学#体系数学問題集3(論理・確率編)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
√2が無理数であることを用いて「1＋2√2が無理数である」ことを証明せよ【背理法】
この動画を見る
√2が無理数であることを用いて「1＋2√2が無理数である」ことを証明せよ【背理法】
【数Ⅰ】体系問題集3(論理・確率編)29：集合と命題：命題と証明：逆裏対偶の真偽の見分け方
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#体系数学#体系数学問題集3(論理・確率編)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
命題［xy＞0 ⇒ x＞0 かつy＞0］の逆、裏、対偶を述べ、さらにそれぞれの真偽を考えよ【集合と命題】【逆 裏 対偶】
この動画を見る
命題［xy＞0 ⇒ x＞0 かつy＞0］の逆、裏、対偶を述べ、さらにそれぞれの真偽を考えよ【集合と命題】【逆 裏 対偶】
【数Ⅰ】体系問題集3(論理・確率編)17：集合と命題：命題と条件：範囲を利用した真偽の見分け方
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
教材：
#体系数学#体系数学問題集3(論理・確率編)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の命題の真偽を調べよ
「-1＜x＜2」 ⇒ 「x＞-2」【集合と命題】
この動画を見る
次の命題の真偽を調べよ
「-1＜x＜2」 ⇒ 「x＞-2」【集合と命題】