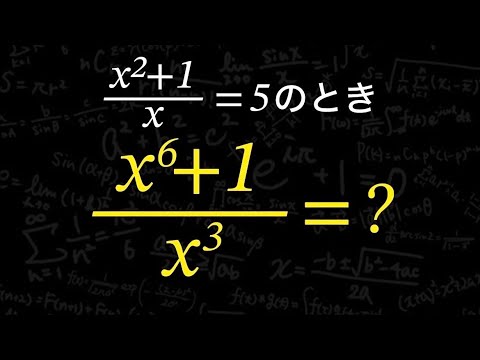#北海道大学1957#方程式_65

問題文全文(内容文)：
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.

1957北海道大学過去問題

単元： #数Ⅰ#大学入試過去問(数学)#数と式#２次関数#一次不等式（不等式・絶対値のある方程式・不等式）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学

指導講師：ますただ

問題文全文(内容文)：
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.

1957北海道大学過去問題

投稿日：2024.10.08

単元： #数学(中学生)#中３数学#数Ⅰ#２次関数#2次関数#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
何を折っているでしょう？

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$

この動画を見る　

単元： #数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
3辺の長さが$a , 2a , a^2$の直角三角形がある。
この三角形の面積を求めよ。
（1 < a < 2）

江戸川学園取手高等学校

この動画を見る　

単元： #数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
軸が直線x=-2で、2点(0,3),(-1,0)を通る。

この動画を見る　

単元： #数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比（内分・外分・二等分線）#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$

この動画を見る　