 一次不等式(不等式・絶対値のある方程式・不等式)
一次不等式(不等式・絶対値のある方程式・不等式)
 一次不等式(不等式・絶対値のある方程式・不等式)
一次不等式(不等式・絶対値のある方程式・不等式)
どっちが難しい?智弁対決 智弁学園VS智弁和歌山

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xの不等式において定数aの値の範囲は?
・$4x \leqq 5-3a$の解が自然数を1つも含まないとき 2001智辯学園高等学校
・x<aを満たす自然数xがちょうど3コのとき 2002智辯学園和歌山高等学校
この動画を見る
xの不等式において定数aの値の範囲は?
・$4x \leqq 5-3a$の解が自然数を1つも含まないとき 2001智辯学園高等学校
・x<aを満たす自然数xがちょうど3コのとき 2002智辯学園和歌山高等学校
Xが消える。。。解けない!?不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式を解け
(1)$x>x$
(2)$x \geqq x$
(3)$x+1>x$
(4)$x>x+1$
この動画を見る
不等式を解け
(1)$x>x$
(2)$x \geqq x$
(3)$x+1>x$
(4)$x>x+1$
不等式 順天堂大

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x$についての不等式
$ax+5>4a+1$の解が$x=3$を含むとき、定数$a$の値の範囲を求めよ
順天堂大学
この動画を見る
$x$についての不等式
$ax+5>4a+1$の解が$x=3$を含むとき、定数$a$の値の範囲を求めよ
順天堂大学
2024年共通テスト速報〜数学ⅠA第1問の(1)〜福田の入試解説

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
この動画を見る
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
【共通テスト】数学IA 第1問で満点取る思考回路、解説します(2023年本試)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数学IA 第1問で満点取る思考回路、解説
(1)
実数$x$についての不等式$|x+6| \leqq 2$の解は[アイ]$ \leqq x \leqq $[ウエ]である。
よって実数$a,b,c,d$が$|(1-\sqrt{ 3 }(a-b)(c-d)+6|\leqq 2$を満たしているとき、
$1-\sqrt{ 3 }$は負であることに注意すると、$(a-b)(c-d)$のとり得る値の範囲は
[オ]+[カ]$\sqrt{ 3 } \leqq (a-b)(c-d) \leqq$[キ]+[ク]$\sqrt{ 3 }$であることがわかる。
$(a-b)(c-d)=$[キ]+[ク]$\sqrt{ 3 }$・・・・①
であるとき、さらに
$(a-b)(c-d)=-3+\sqrt{ 3 }$・・・・②
が成り立つならば
$(a-b)(c-d)=$[ケ]+[コ]$\sqrt{ 3 }$・・・・③
であることが、等式①、②、③の左辺を展開して比較することによりわかる。
(2)
点Oを中心とし、半径が5である円0がある。
この円周上に2点A,BをAB=6となるようにとる。
また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
①$\sin \angle ACB =$[サ]である。また、点Cを$\angle ACB$が純角となるようにとるとき、$\cos \angle ACB =$[シ]である。
②点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直角ABに垂直な直線を引き、直線ABとの交点をDとするとき、$\tan \angle OAD =$[ス]である。
また、$\triangle ABC$の面積は[セソ]である。
この動画を見る
【共通テスト】数学IA 第1問で満点取る思考回路、解説
(1)
実数$x$についての不等式$|x+6| \leqq 2$の解は[アイ]$ \leqq x \leqq $[ウエ]である。
よって実数$a,b,c,d$が$|(1-\sqrt{ 3 }(a-b)(c-d)+6|\leqq 2$を満たしているとき、
$1-\sqrt{ 3 }$は負であることに注意すると、$(a-b)(c-d)$のとり得る値の範囲は
[オ]+[カ]$\sqrt{ 3 } \leqq (a-b)(c-d) \leqq$[キ]+[ク]$\sqrt{ 3 }$であることがわかる。
$(a-b)(c-d)=$[キ]+[ク]$\sqrt{ 3 }$・・・・①
であるとき、さらに
$(a-b)(c-d)=-3+\sqrt{ 3 }$・・・・②
が成り立つならば
$(a-b)(c-d)=$[ケ]+[コ]$\sqrt{ 3 }$・・・・③
であることが、等式①、②、③の左辺を展開して比較することによりわかる。
(2)
点Oを中心とし、半径が5である円0がある。
この円周上に2点A,BをAB=6となるようにとる。
また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
①$\sin \angle ACB =$[サ]である。また、点Cを$\angle ACB$が純角となるようにとるとき、$\cos \angle ACB =$[シ]である。
②点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直角ABに垂直な直線を引き、直線ABとの交点をDとするとき、$\tan \angle OAD =$[ス]である。
また、$\triangle ABC$の面積は[セソ]である。
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
=入れる入れない問題。不等式。初見でよく間違えます。高知学芸

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式1< x < k+2を満たす整数xが2と3だけであるときkの範囲を求めよ。
高知学芸高等学校
この動画を見る
不等式1< x < k+2を満たす整数xが2と3だけであるときkの範囲を求めよ。
高知学芸高等学校
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
三角比の不等式

単元:
#数Ⅰ#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式を解け
$sinθ \leqq cosθ$
$(0° \leqq θ < 360°)$
この動画を見る
不等式を解け
$sinθ \leqq cosθ$
$(0° \leqq θ < 360°)$
Xが消える 不等式

等式の変形 國學院久我山
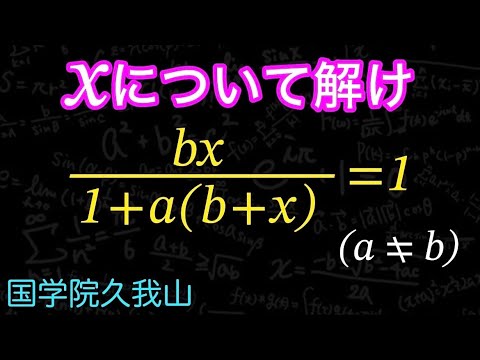
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xについて解け
$\frac{bx}{1+a(b+x)}=1$ $(a \neq b)$
國學院大學久我山高等学校
この動画を見る
xについて解け
$\frac{bx}{1+a(b+x)}=1$ $(a \neq b)$
國學院大學久我山高等学校
引っかかりやすい指数不等式

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式を解け
$-8 \leqq 2^x \leqq 8$
この動画を見る
不等式を解け
$-8 \leqq 2^x \leqq 8$
絶対値だけど場合分け不要。4通りで解説。

青山学院大 放物線の中の四角形

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#図形の性質#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
この動画を見る
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
関西医科大 分数不等式 整数問題

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022関西医科大学過去問題
$f(x)=\frac{6x^2+17x+10}{3x-2}$
①$f(x)>0$をみたすxの範囲
②f(n)が正の整数となる整数n
この動画を見る
2022関西医科大学過去問題
$f(x)=\frac{6x^2+17x+10}{3x-2}$
①$f(x)>0$をみたすxの範囲
②f(n)が正の整数となる整数n
【ホーン・フィールドがていねいに解説】数と式 4S数学問題集数Ⅰ 83,84,85 1次不等式の利用2
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題83
1個800円の品物がある。入会金500円を払って会員になると、この品物を6%引きで買うことができる。入会して品物を買う場合、何個以上買えば入会しないで買うより安くなるか。ただし、消費税は考えないものとする。
問題84
13%と5%の食塩水を混ぜて400gの食塩水を作った。その濃度が10%以上であるとき、混ぜた5%の食塩水は何g以下か。
問題85
ある高等学校の1年全員が長いすに座っていくとき、1脚に6人ずつ座っていくと15人が座れなくなる。また、1脚に7人ずつ座っていくと、使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
この動画を見る
問題83
1個800円の品物がある。入会金500円を払って会員になると、この品物を6%引きで買うことができる。入会して品物を買う場合、何個以上買えば入会しないで買うより安くなるか。ただし、消費税は考えないものとする。
問題84
13%と5%の食塩水を混ぜて400gの食塩水を作った。その濃度が10%以上であるとき、混ぜた5%の食塩水は何g以下か。
問題85
ある高等学校の1年全員が長いすに座っていくとき、1脚に6人ずつ座っていくと15人が座れなくなる。また、1脚に7人ずつ座っていくと、使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
場合分け不要!!絶対値を含む不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1) $|x-1|<2$
(2) $|x-1|<2x$
不等式を解け
この動画を見る
(1) $|x-1|<2$
(2) $|x-1|<2x$
不等式を解け
式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
この動画を見る
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
絶対値を含む方程式
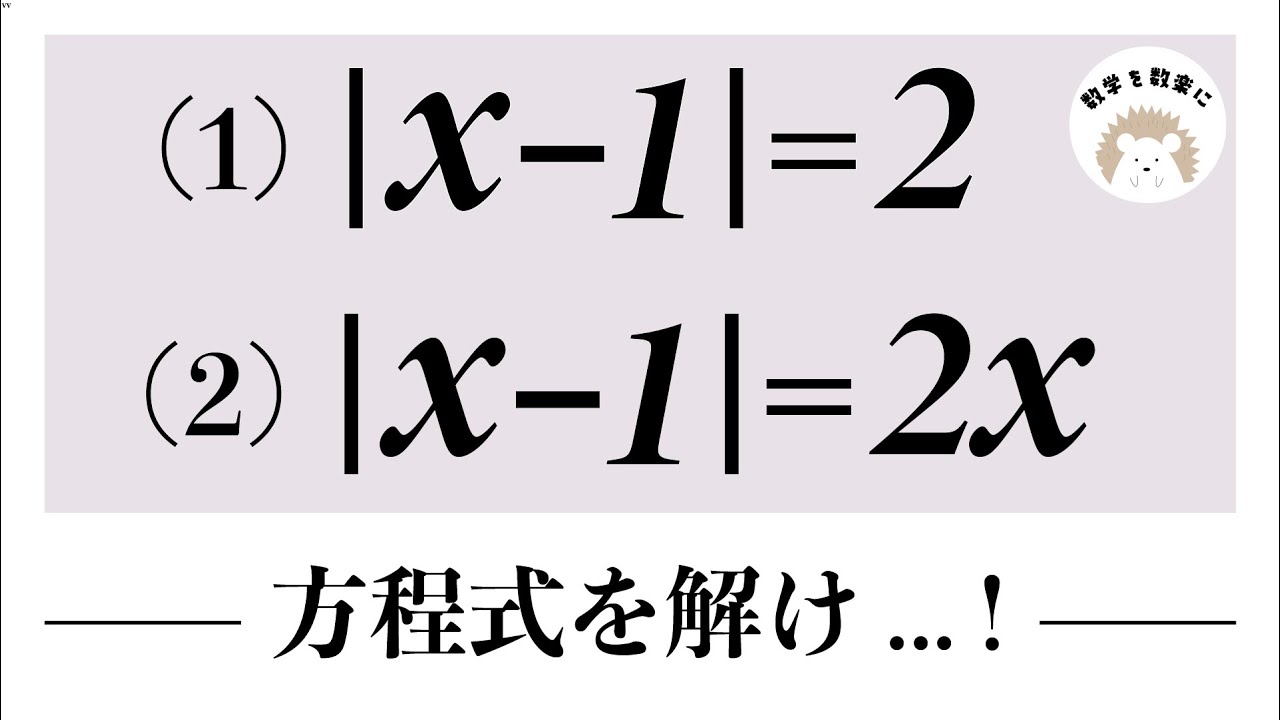
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
この動画を見る
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
対数と不等式

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
この動画を見る
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
神戸大 不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
この動画を見る
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
数と式 1次不等式の利用【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
この動画を見る
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
神戸大 3次方程式の基本問題
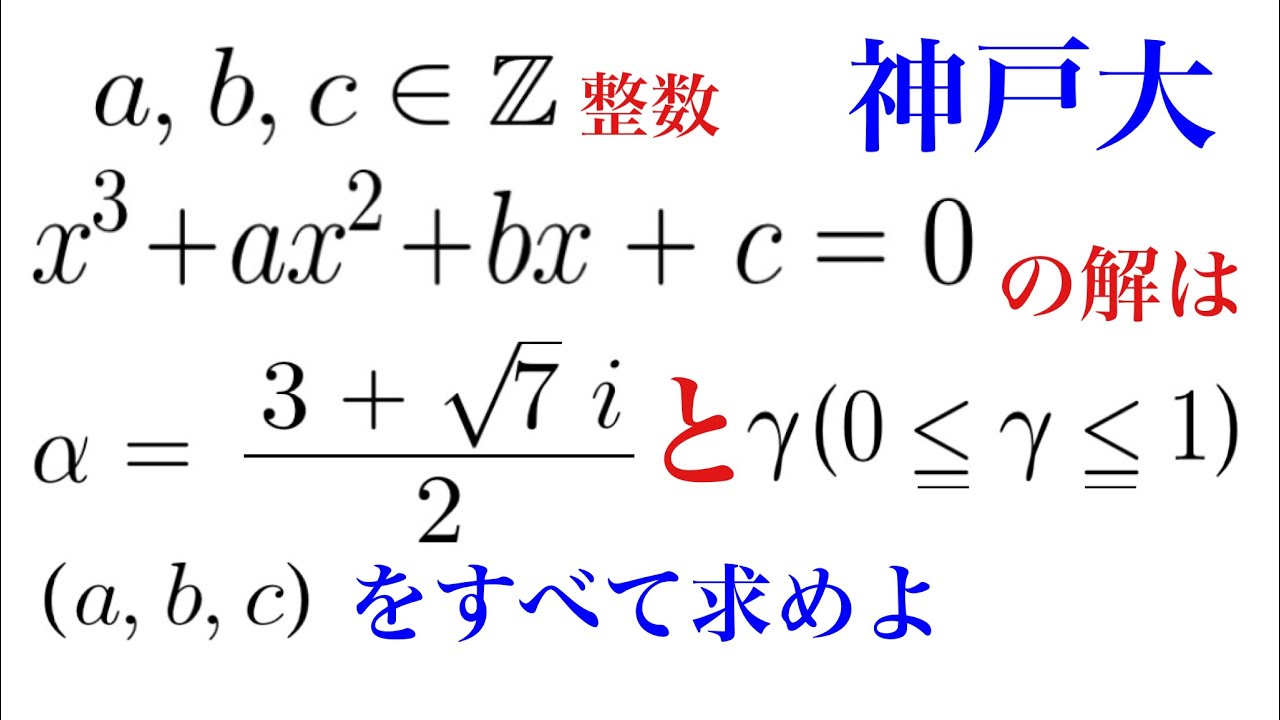
単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式(不等式・絶対値のある方程式・不等式)#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
この動画を見る
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
根号を含んだ不等式の証明

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a>0,b>0$のとき
$3 \sqrt a + 2 \sqrt b > \sqrt {9a+4b}$
を示せ
この動画を見る
$a>0,b>0$のとき
$3 \sqrt a + 2 \sqrt b > \sqrt {9a+4b}$
を示せ
福田の数学〜慶應義塾大学2023年薬学部第1問(3)〜3次関数と絶対不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
知っていれば一瞬!絶対値の入った2次方程式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2 - 4|x| - 12 = 0$を解け
この動画を見る
$x^2 - 4|x| - 12 = 0$を解け
ルートと絶対値の入っている連立不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連立不等式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
(2 - \sqrt 5 )x > -1 \\
|3x-5| < 8
\end{array}
\right.
\end{eqnarray}
この動画を見る
連立不等式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
(2 - \sqrt 5 )x > -1 \\
|3x-5| < 8
\end{array}
\right.
\end{eqnarray}
x二乗をかけろ
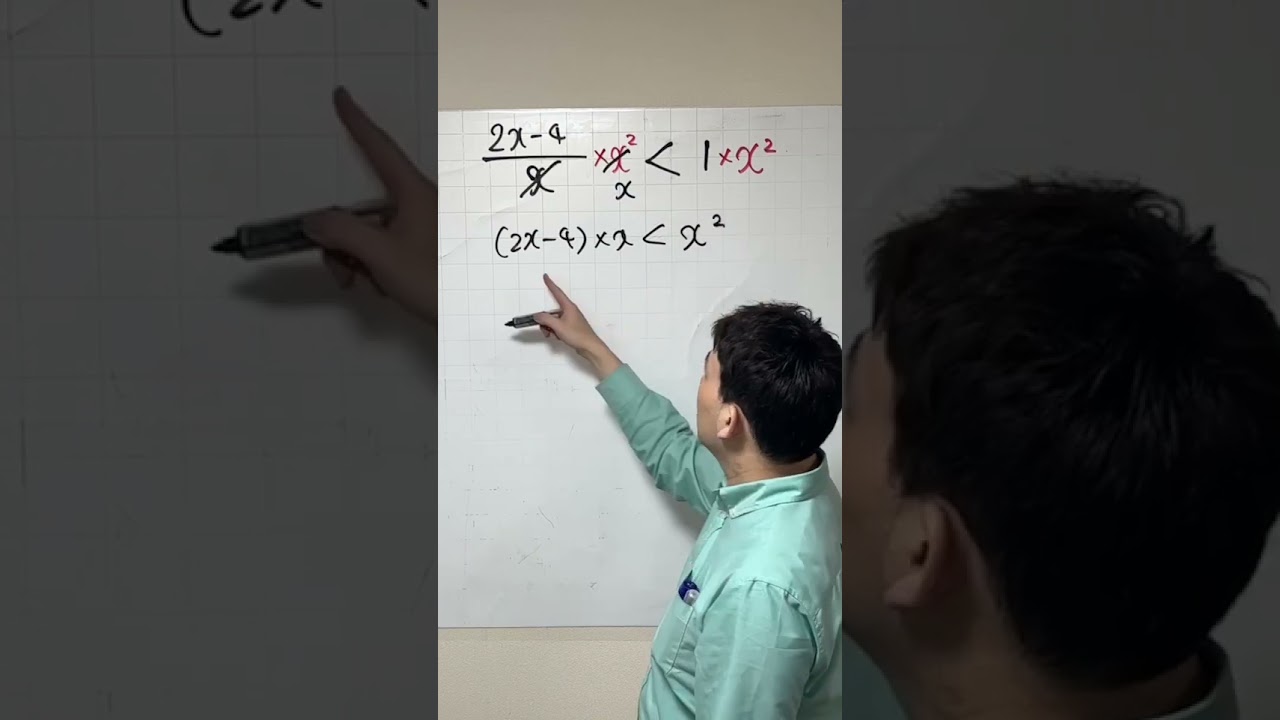
誰もが一度は間違える

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2x-4}{x} = 1$
$\frac{2x-4}{x} < 1$
この動画を見る
$\frac{2x-4}{x} = 1$
$\frac{2x-4}{x} < 1$
福田の1.5倍速演習〜合格する重要問題101〜慶應義塾大学2020年度環境情報学部第1問(1)〜不定方程式の解

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#平面上の曲線#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#加法定理とその応用#2次曲線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)正の実数xとyが9$x^2$+16$y^2$=144 を満たしているとき、xyの最大値は$\boxed{\ \ アイ\ \ }$である。
2020慶應義塾大学環境情報学部過去問
この動画を見る
$\Large\boxed{1}$ (1)正の実数xとyが9$x^2$+16$y^2$=144 を満たしているとき、xyの最大値は$\boxed{\ \ アイ\ \ }$である。
2020慶應義塾大学環境情報学部過去問
