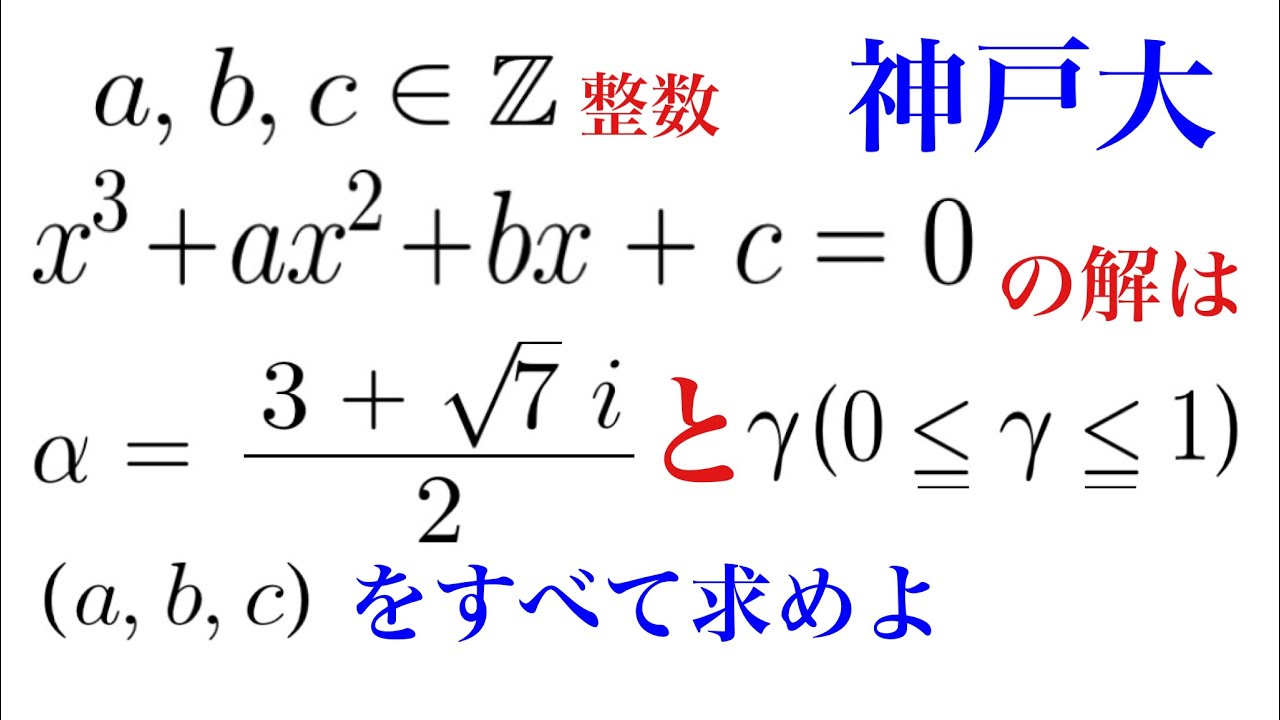問題文全文(内容文):
'92名古屋大学過去問題
$α=\frac{1-\sqrt7 i}{2},β=\frac{1+\sqrt7 i}{2}$
(1)次の等式を示せ。n自然数
$α^{n+1}+β^{n+1}=α^n+β^n-2(α^{n-1}+β^{n-1})$
(2)$α^n+β^n$が奇数であることを示せ。n自然数
'92名古屋大学過去問題
$α=\frac{1-\sqrt7 i}{2},β=\frac{1+\sqrt7 i}{2}$
(1)次の等式を示せ。n自然数
$α^{n+1}+β^{n+1}=α^n+β^n-2(α^{n-1}+β^{n-1})$
(2)$α^n+β^n$が奇数であることを示せ。n自然数
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
'92名古屋大学過去問題
$α=\frac{1-\sqrt7 i}{2},β=\frac{1+\sqrt7 i}{2}$
(1)次の等式を示せ。n自然数
$α^{n+1}+β^{n+1}=α^n+β^n-2(α^{n-1}+β^{n-1})$
(2)$α^n+β^n$が奇数であることを示せ。n自然数
'92名古屋大学過去問題
$α=\frac{1-\sqrt7 i}{2},β=\frac{1+\sqrt7 i}{2}$
(1)次の等式を示せ。n自然数
$α^{n+1}+β^{n+1}=α^n+β^n-2(α^{n-1}+β^{n-1})$
(2)$α^n+β^n$が奇数であることを示せ。n自然数
投稿日:2018.11.19