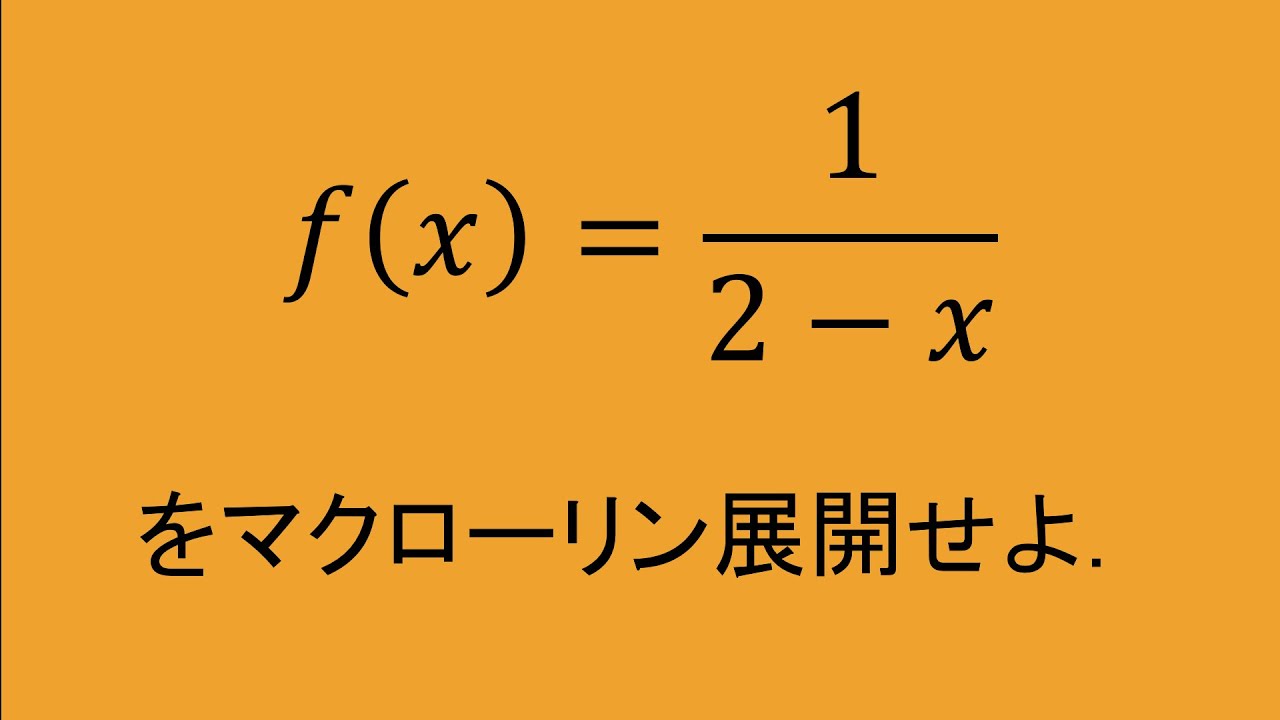問題文全文(内容文):
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
投稿日:2020.11.07