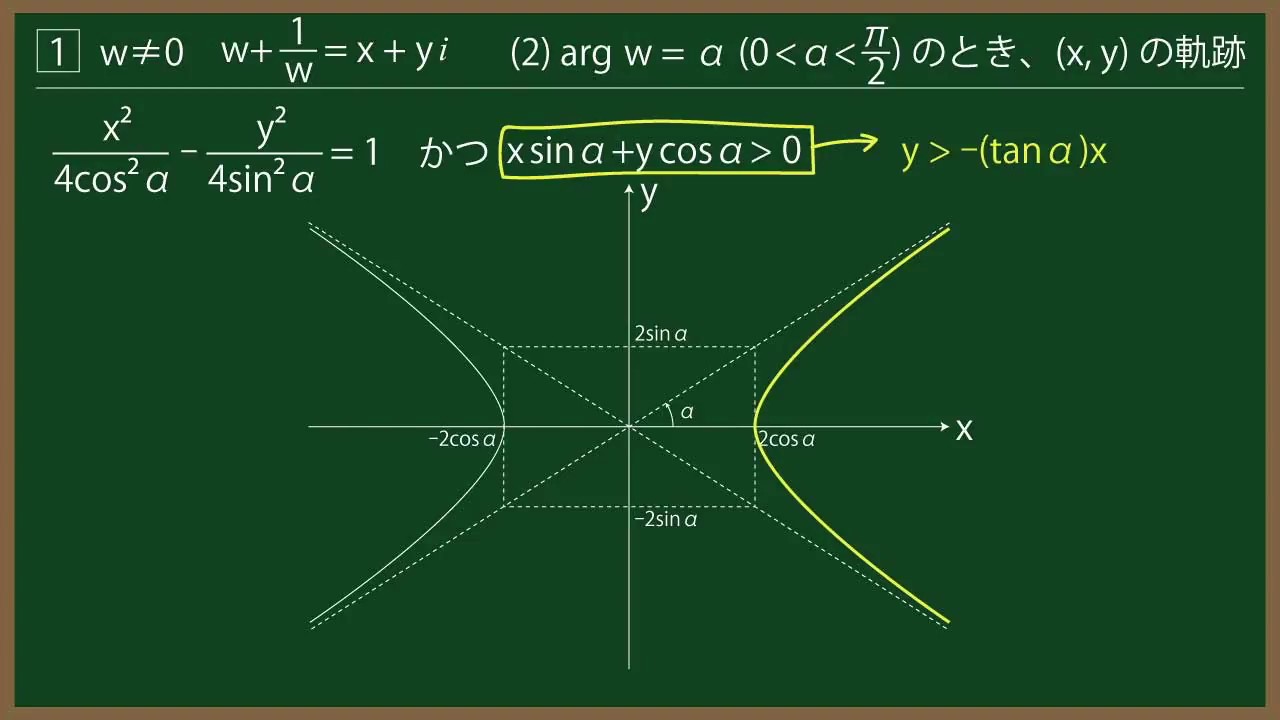
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{3}}\ 複素数平面上に、原点Oを頂点の1つとする正六角形OABCDEが与えられている。\\
ただしその頂点は時計の針の進む方向と逆向きにO,A,B,C,D,Eとする。\\
互いに異なる0でない複素数\alpha,\beta,\gammaが、\\
0 \leqq \arg(\frac{\beta}{\alpha}) \leqq \pi, 4\alpha^2-2\alpha\beta+\beta^2=0, 2\gamma^2-(3\alpha+\beta+2)\gamma+(\alpha+1)(\alpha+\beta)=0\\
を満たし、\alpha,\beta,\gammaのそれぞれが正六角形OABCDEの頂点のいずれかであるとする。\\
(1)\frac{\beta}{\alpha}を求め、\alpha,\betaがそれぞれどの頂点か答えよ。\\
(2)組(\alpha,\beta,\gamma)を全て求め、それぞれの組について正六角形OABCDEを\\
複素数平面上に図示せよ。
\end{eqnarray}
\begin{eqnarray}
{\Large\boxed{3}}\ 複素数平面上に、原点Oを頂点の1つとする正六角形OABCDEが与えられている。\\
ただしその頂点は時計の針の進む方向と逆向きにO,A,B,C,D,Eとする。\\
互いに異なる0でない複素数\alpha,\beta,\gammaが、\\
0 \leqq \arg(\frac{\beta}{\alpha}) \leqq \pi, 4\alpha^2-2\alpha\beta+\beta^2=0, 2\gamma^2-(3\alpha+\beta+2)\gamma+(\alpha+1)(\alpha+\beta)=0\\
を満たし、\alpha,\beta,\gammaのそれぞれが正六角形OABCDEの頂点のいずれかであるとする。\\
(1)\frac{\beta}{\alpha}を求め、\alpha,\betaがそれぞれどの頂点か答えよ。\\
(2)組(\alpha,\beta,\gamma)を全て求め、それぞれの組について正六角形OABCDEを\\
複素数平面上に図示せよ。
\end{eqnarray}
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数C
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{3}}\ 複素数平面上に、原点Oを頂点の1つとする正六角形OABCDEが与えられている。\\
ただしその頂点は時計の針の進む方向と逆向きにO,A,B,C,D,Eとする。\\
互いに異なる0でない複素数\alpha,\beta,\gammaが、\\
0 \leqq \arg(\frac{\beta}{\alpha}) \leqq \pi, 4\alpha^2-2\alpha\beta+\beta^2=0, 2\gamma^2-(3\alpha+\beta+2)\gamma+(\alpha+1)(\alpha+\beta)=0\\
を満たし、\alpha,\beta,\gammaのそれぞれが正六角形OABCDEの頂点のいずれかであるとする。\\
(1)\frac{\beta}{\alpha}を求め、\alpha,\betaがそれぞれどの頂点か答えよ。\\
(2)組(\alpha,\beta,\gamma)を全て求め、それぞれの組について正六角形OABCDEを\\
複素数平面上に図示せよ。
\end{eqnarray}
\begin{eqnarray}
{\Large\boxed{3}}\ 複素数平面上に、原点Oを頂点の1つとする正六角形OABCDEが与えられている。\\
ただしその頂点は時計の針の進む方向と逆向きにO,A,B,C,D,Eとする。\\
互いに異なる0でない複素数\alpha,\beta,\gammaが、\\
0 \leqq \arg(\frac{\beta}{\alpha}) \leqq \pi, 4\alpha^2-2\alpha\beta+\beta^2=0, 2\gamma^2-(3\alpha+\beta+2)\gamma+(\alpha+1)(\alpha+\beta)=0\\
を満たし、\alpha,\beta,\gammaのそれぞれが正六角形OABCDEの頂点のいずれかであるとする。\\
(1)\frac{\beta}{\alpha}を求め、\alpha,\betaがそれぞれどの頂点か答えよ。\\
(2)組(\alpha,\beta,\gamma)を全て求め、それぞれの組について正六角形OABCDEを\\
複素数平面上に図示せよ。
\end{eqnarray}
投稿日:2022.04.10