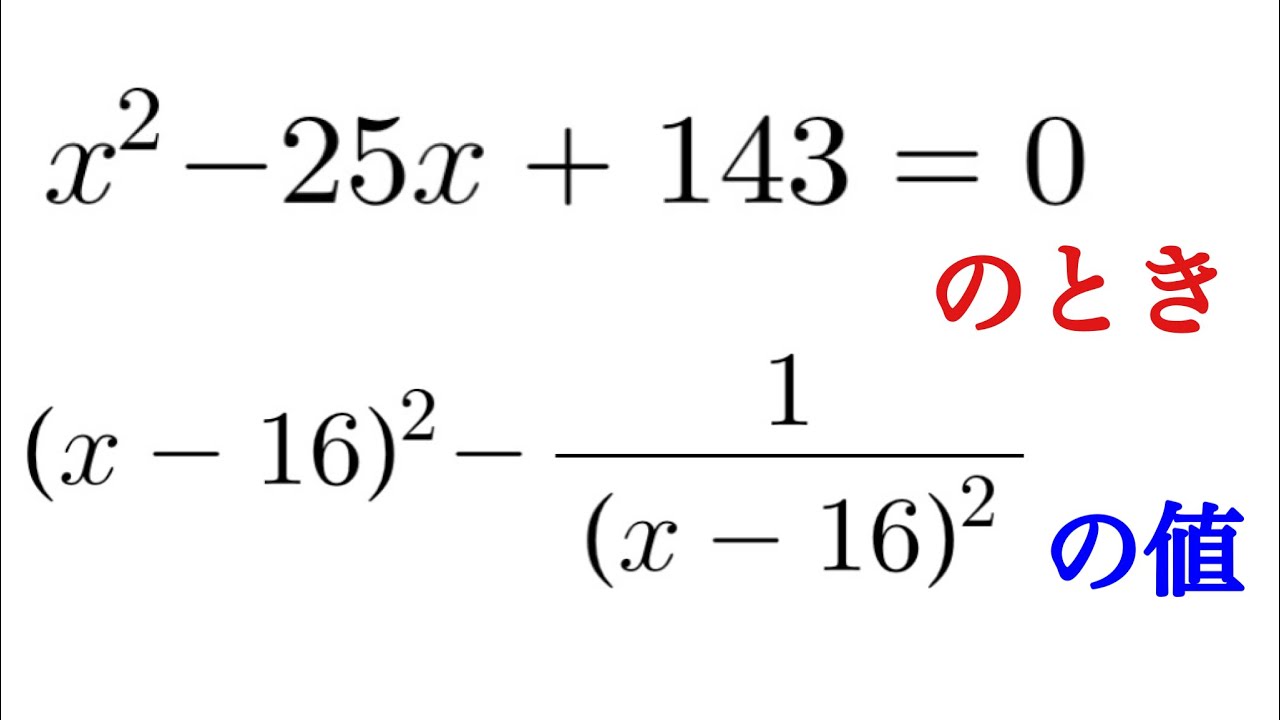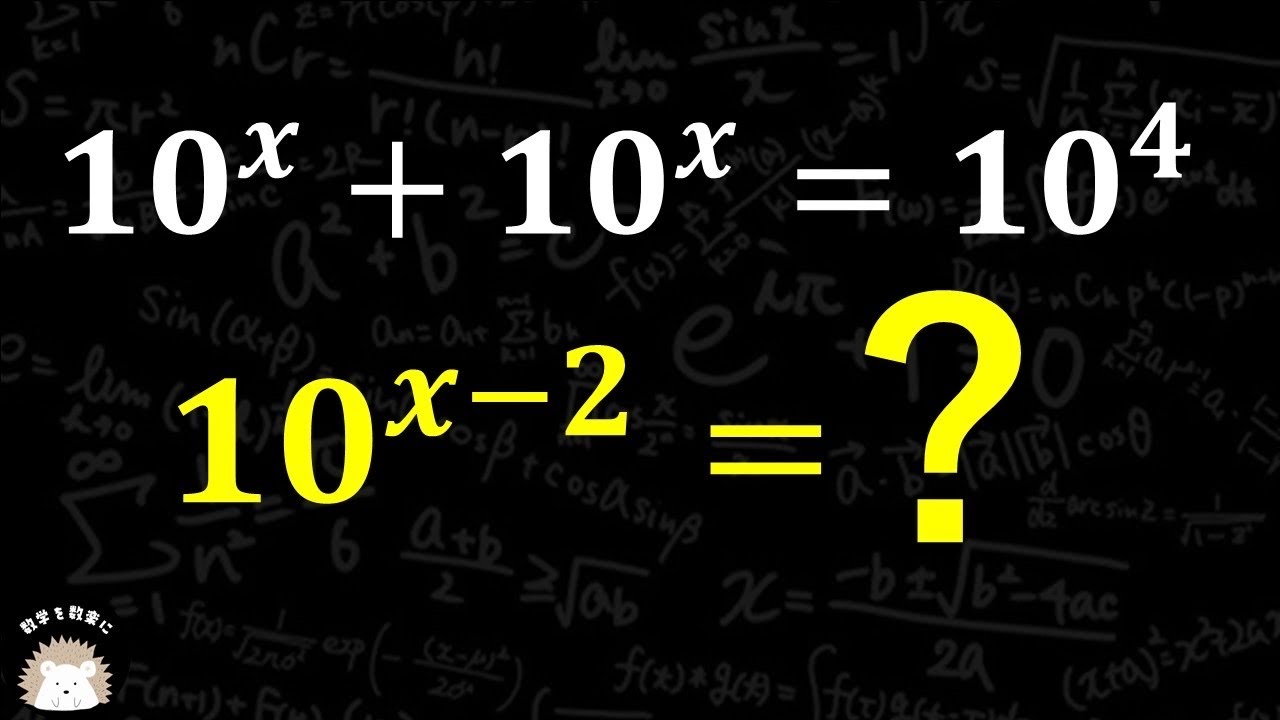問題文全文(内容文):
${\large\boxed{4}}$自然数$a,b$に対し、3次関数$f_{a,b}(x),g_{a,b}(x)$を
$f_{a,b}(x)=x^3+3ax^2+3bx+8$
$g_{a,b}(x)=8x^3+3bx^2+3ax+1$
で定める。次の問いに答えよ。
(1)次の条件$(\textrm{I})(\textrm{II})$の両方を満たす自然数の組(a,b)
で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{I})f_{a,b}(x)$が極値をもつ
$(\textrm{II})g_{a,b}(x)$が極値をもつ
(2)3次方程式$f_{a,b}(x)=0$の3つの解が$\alpha,\beta,\gamma$であるとき
3次方程式$g_{a,b}(x)=0$の解を$\alpha,\beta,\gamma$で表せ。
(3)次の条件$(\textrm{III})$を満たす自然数の組$(a,b)$で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{III})$3次方程式$f_{a,b}(x)=0$が相異なる3つの実数解をもつ。
2022早稲田大学教育学部過去問
${\large\boxed{4}}$自然数$a,b$に対し、3次関数$f_{a,b}(x),g_{a,b}(x)$を
$f_{a,b}(x)=x^3+3ax^2+3bx+8$
$g_{a,b}(x)=8x^3+3bx^2+3ax+1$
で定める。次の問いに答えよ。
(1)次の条件$(\textrm{I})(\textrm{II})$の両方を満たす自然数の組(a,b)
で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{I})f_{a,b}(x)$が極値をもつ
$(\textrm{II})g_{a,b}(x)$が極値をもつ
(2)3次方程式$f_{a,b}(x)=0$の3つの解が$\alpha,\beta,\gamma$であるとき
3次方程式$g_{a,b}(x)=0$の解を$\alpha,\beta,\gamma$で表せ。
(3)次の条件$(\textrm{III})$を満たす自然数の組$(a,b)$で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{III})$3次方程式$f_{a,b}(x)=0$が相異なる3つの実数解をもつ。
2022早稲田大学教育学部過去問
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$自然数$a,b$に対し、3次関数$f_{a,b}(x),g_{a,b}(x)$を
$f_{a,b}(x)=x^3+3ax^2+3bx+8$
$g_{a,b}(x)=8x^3+3bx^2+3ax+1$
で定める。次の問いに答えよ。
(1)次の条件$(\textrm{I})(\textrm{II})$の両方を満たす自然数の組(a,b)
で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{I})f_{a,b}(x)$が極値をもつ
$(\textrm{II})g_{a,b}(x)$が極値をもつ
(2)3次方程式$f_{a,b}(x)=0$の3つの解が$\alpha,\beta,\gamma$であるとき
3次方程式$g_{a,b}(x)=0$の解を$\alpha,\beta,\gamma$で表せ。
(3)次の条件$(\textrm{III})$を満たす自然数の組$(a,b)$で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{III})$3次方程式$f_{a,b}(x)=0$が相異なる3つの実数解をもつ。
2022早稲田大学教育学部過去問
${\large\boxed{4}}$自然数$a,b$に対し、3次関数$f_{a,b}(x),g_{a,b}(x)$を
$f_{a,b}(x)=x^3+3ax^2+3bx+8$
$g_{a,b}(x)=8x^3+3bx^2+3ax+1$
で定める。次の問いに答えよ。
(1)次の条件$(\textrm{I})(\textrm{II})$の両方を満たす自然数の組(a,b)
で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{I})f_{a,b}(x)$が極値をもつ
$(\textrm{II})g_{a,b}(x)$が極値をもつ
(2)3次方程式$f_{a,b}(x)=0$の3つの解が$\alpha,\beta,\gamma$であるとき
3次方程式$g_{a,b}(x)=0$の解を$\alpha,\beta,\gamma$で表せ。
(3)次の条件$(\textrm{III})$を満たす自然数の組$(a,b)$で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{III})$3次方程式$f_{a,b}(x)=0$が相異なる3つの実数解をもつ。
2022早稲田大学教育学部過去問
投稿日:2022.08.14