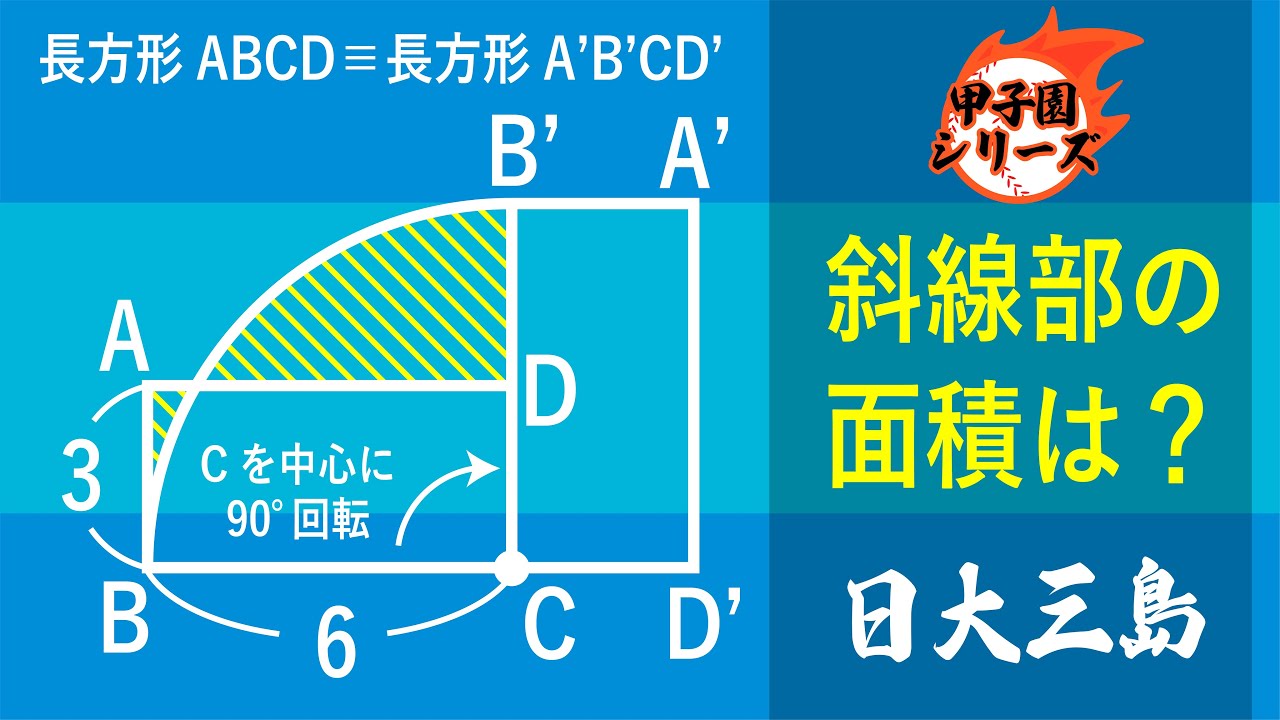
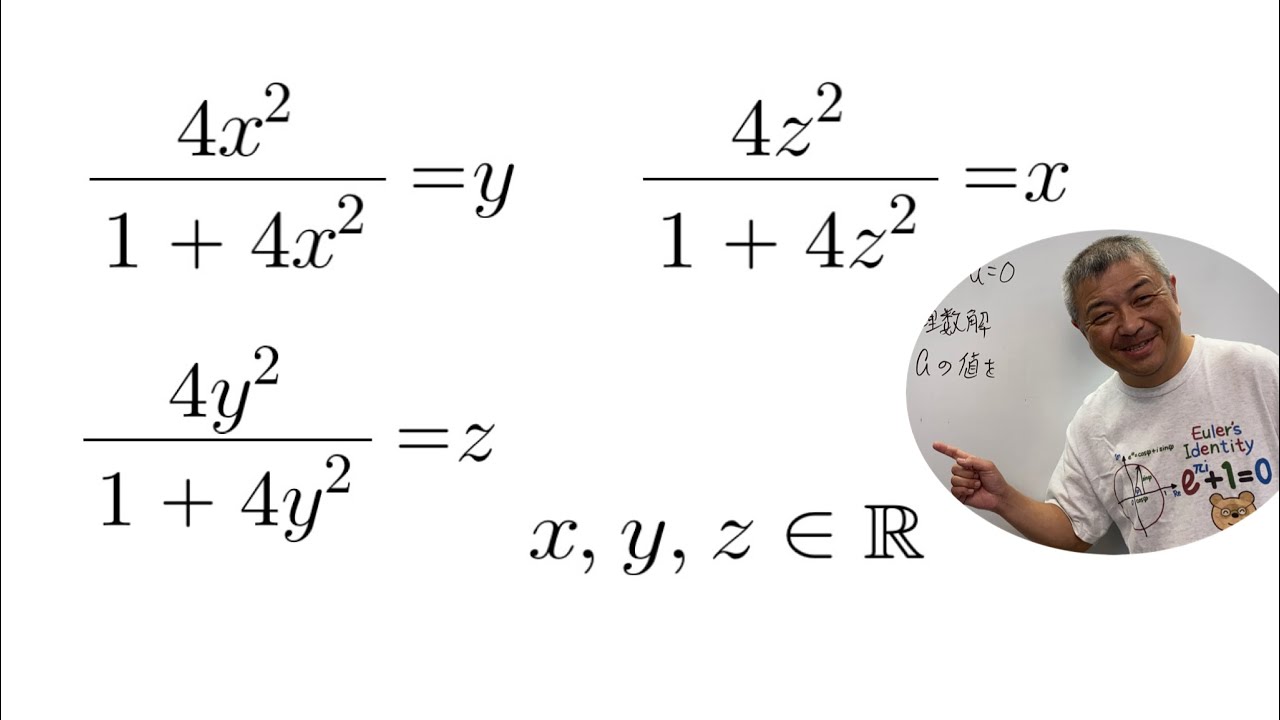問題文全文(内容文):
例1
右の図の$Box ABCD$に,次の条件が加わると,それぞれどんな四角形になりますか?
図形の正確な名前を答えなさい.
(1)$AC=BD$
(2)$AC\perp BD$
(3)$AO=DO,AC\perp BD$
例2
次の四角形$ABCD$は,それぞれどんな四角形になりますか?
図形の正確な名前をこたえなさい.
(1)$\angle A=\angle C,\angle B=\angle D$
(2)$AB /\!/ DC,AB=BC=DC$
(3)$AB=BC=CD=DA,AC=BD$
(4)$AD /\!/ BC,\angle B=\angle D=90°$
例1
右の図の$Box ABCD$に,次の条件が加わると,それぞれどんな四角形になりますか?
図形の正確な名前を答えなさい.
(1)$AC=BD$
(2)$AC\perp BD$
(3)$AO=DO,AC\perp BD$
例2
次の四角形$ABCD$は,それぞれどんな四角形になりますか?
図形の正確な名前をこたえなさい.
(1)$\angle A=\angle C,\angle B=\angle D$
(2)$AB /\!/ DC,AB=BC=DC$
(3)$AB=BC=CD=DA,AC=BD$
(4)$AD /\!/ BC,\angle B=\angle D=90°$
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1
右の図の$Box ABCD$に,次の条件が加わると,それぞれどんな四角形になりますか?
図形の正確な名前を答えなさい.
(1)$AC=BD$
(2)$AC\perp BD$
(3)$AO=DO,AC\perp BD$
例2
次の四角形$ABCD$は,それぞれどんな四角形になりますか?
図形の正確な名前をこたえなさい.
(1)$\angle A=\angle C,\angle B=\angle D$
(2)$AB /\!/ DC,AB=BC=DC$
(3)$AB=BC=CD=DA,AC=BD$
(4)$AD /\!/ BC,\angle B=\angle D=90°$
例1
右の図の$Box ABCD$に,次の条件が加わると,それぞれどんな四角形になりますか?
図形の正確な名前を答えなさい.
(1)$AC=BD$
(2)$AC\perp BD$
(3)$AO=DO,AC\perp BD$
例2
次の四角形$ABCD$は,それぞれどんな四角形になりますか?
図形の正確な名前をこたえなさい.
(1)$\angle A=\angle C,\angle B=\angle D$
(2)$AB /\!/ DC,AB=BC=DC$
(3)$AB=BC=CD=DA,AC=BD$
(4)$AD /\!/ BC,\angle B=\angle D=90°$
投稿日:2023.04.20