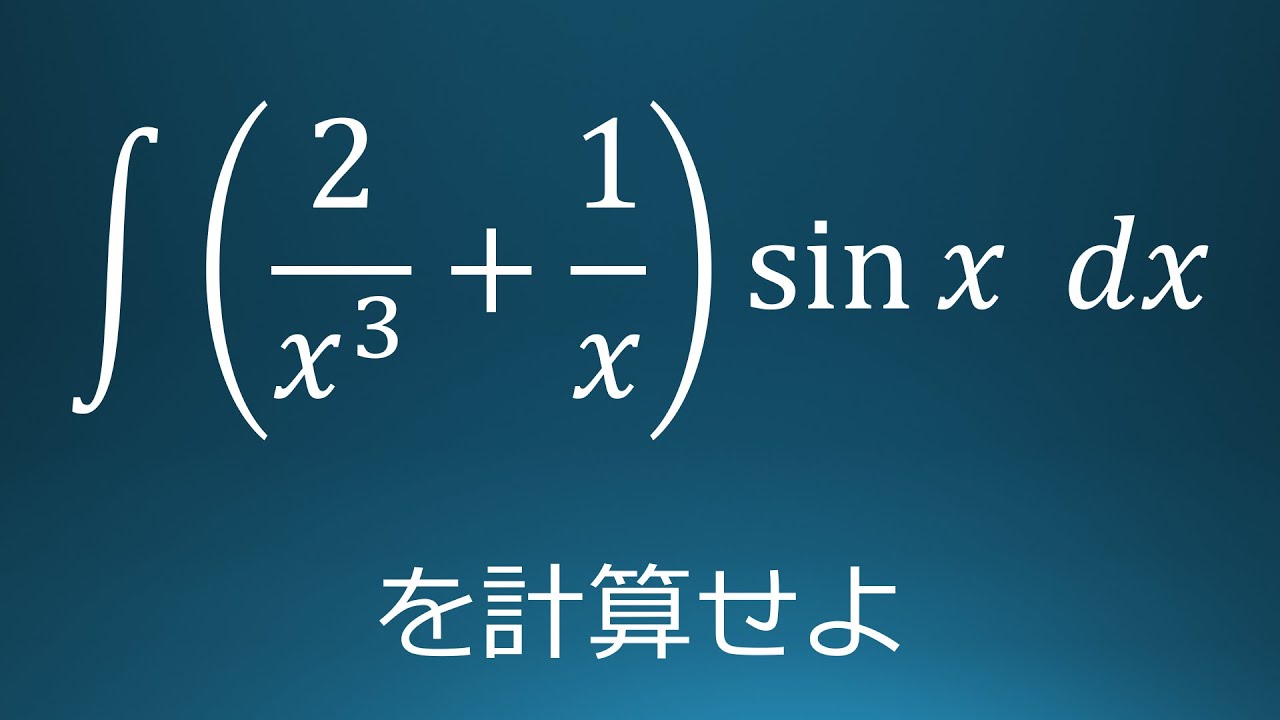福田のおもしろ数学253〜減衰曲線と定積分の極限

問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \int_{(k-1)π}^{ kπ } |e^{-x}sinx| dx$を求めて下さい。

単元： #積分とその応用#面積・体積・長さ・速度#数Ⅲ

指導講師：福田次郎

問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \int_{(k-1)π}^{ kπ } |e^{-x}sinx| dx$を求めて下さい。

投稿日：2024.09.11

単元： #積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
2⃣ $1+\frac{1}{2} + \frac{1}{3} + \cdots +\frac{1}{n} > log(n+1)$を示せ。
$n \in \mathbb{N}$

この動画を見る　

単元： #数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
5⃣
(1)$\int x(x^2+4)^{\frac{1}{3}} dx$
(2)$\int_2^{2\sqrt{15}} x(x^2+4)^{\frac{1}{3}} dx$

この動画を見る　

単元： #積分とその応用#定積分#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\int_1^4\frac{dx}{\sqrt{3-\sqrt{x}}}$
これを解け.

この動画を見る　

単元： #大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^3}{x}(1-log\ x)^4dx$

出典：2019年東京理科大学　入試問題

この動画を見る　

単元： #積分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$\boxed{10}$これを解け.
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin\dfrac{5}{2}x\cos\dfrac{1}{2}x\ dx$

この動画を見る　