問題文全文(内容文):
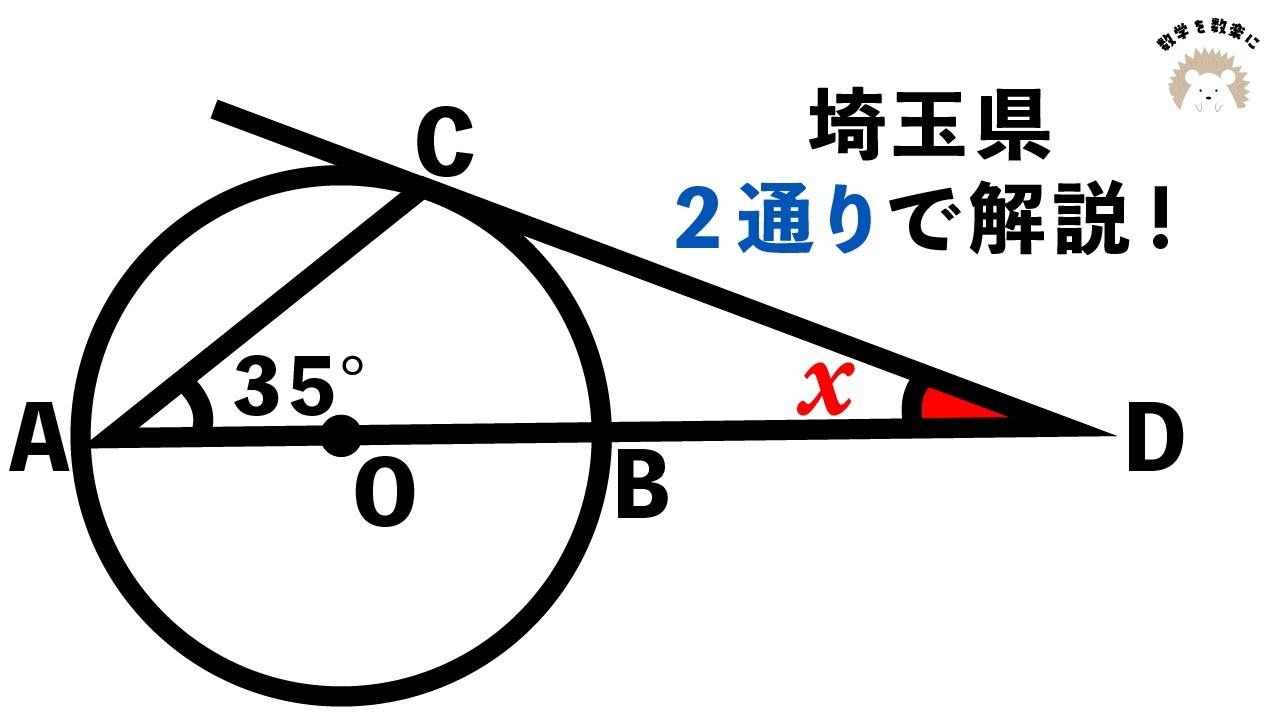
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
チャプター:
0:00 オープニング
0:05 問題文
0:25 解説
1:39 証明
2:59 エンディング
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
投稿日:2023.10.06