問題文全文(内容文):
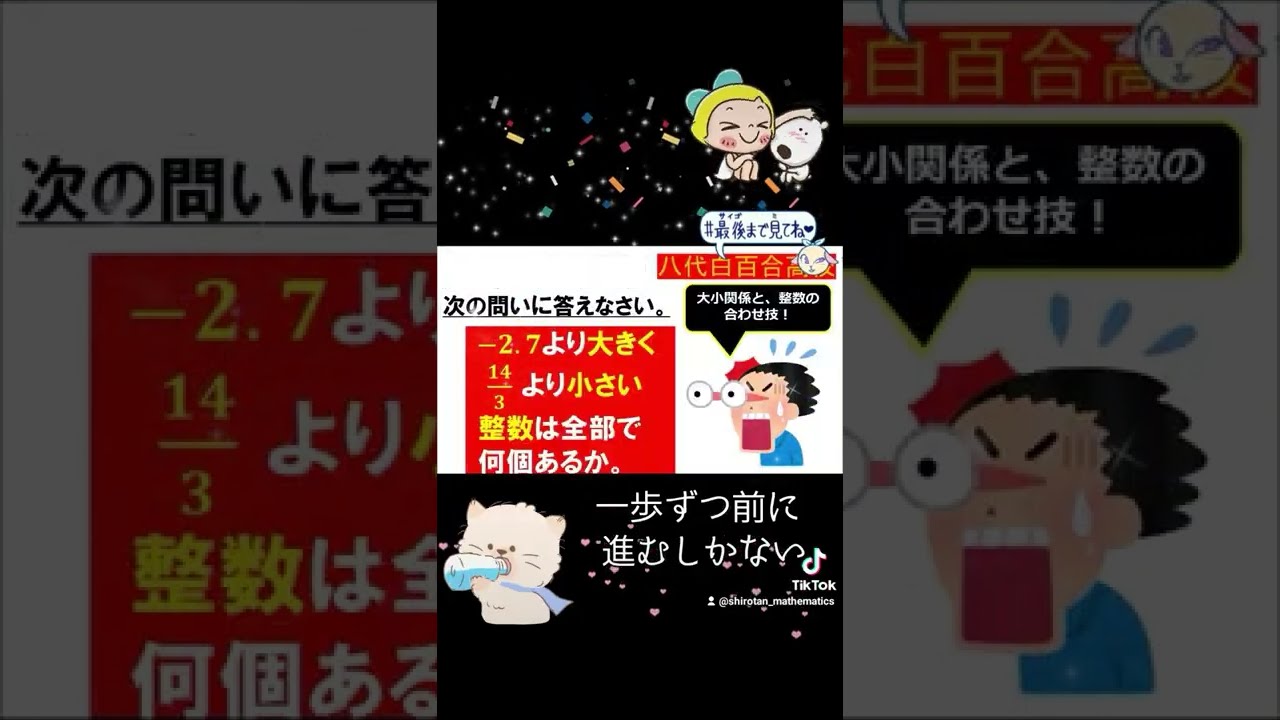
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
単元:
#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#数と式#式と証明#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#恒等式・等式・不等式の証明#文字と式
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
投稿日:2018.07.09