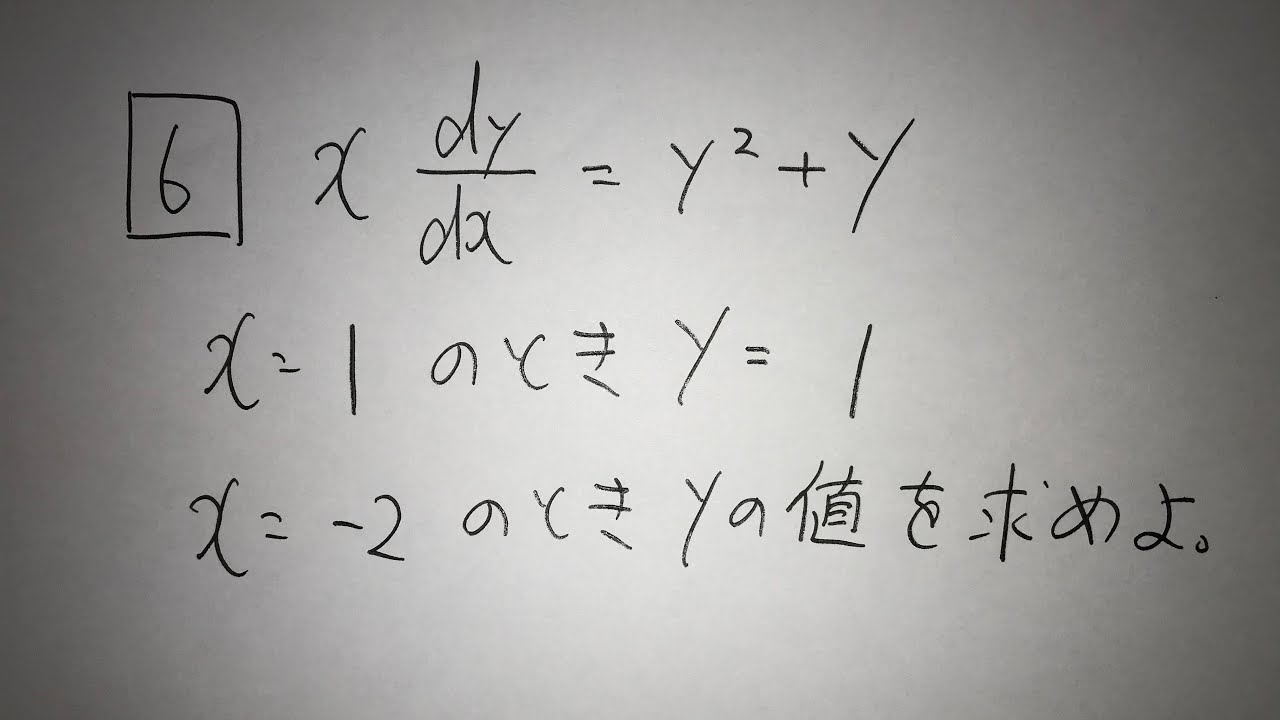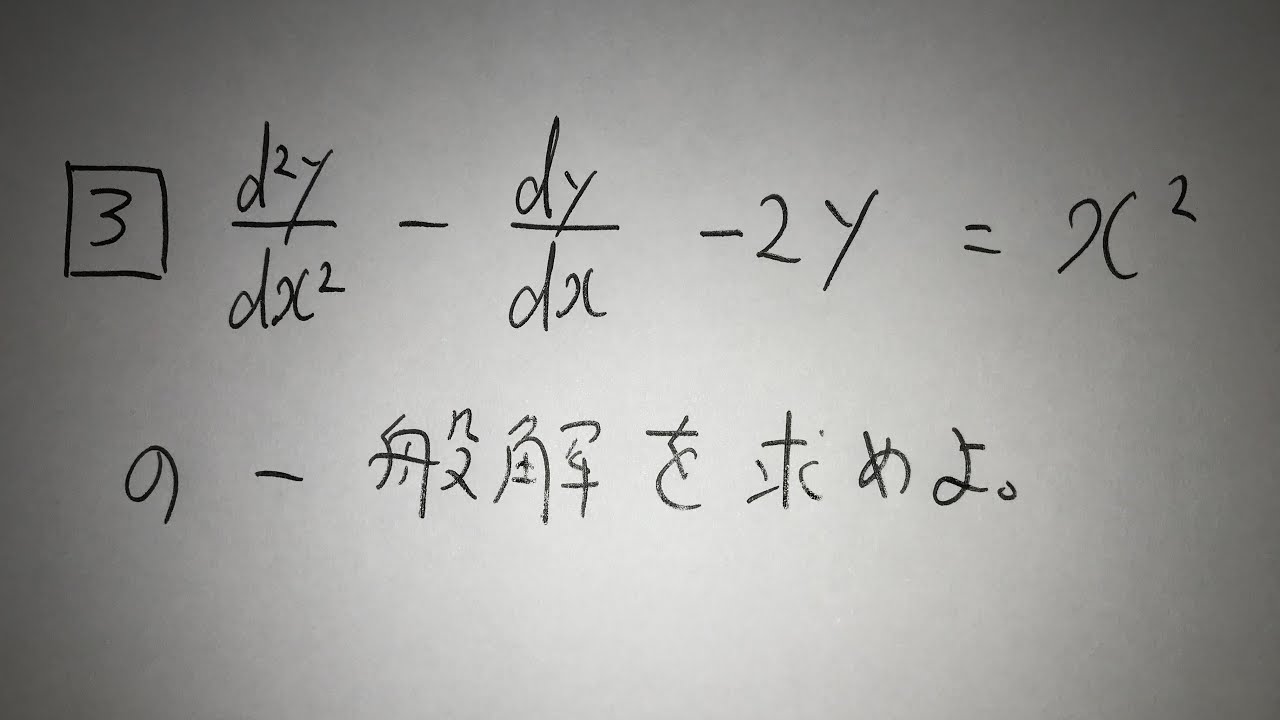問題文全文(内容文):
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
投稿日:2021.07.08