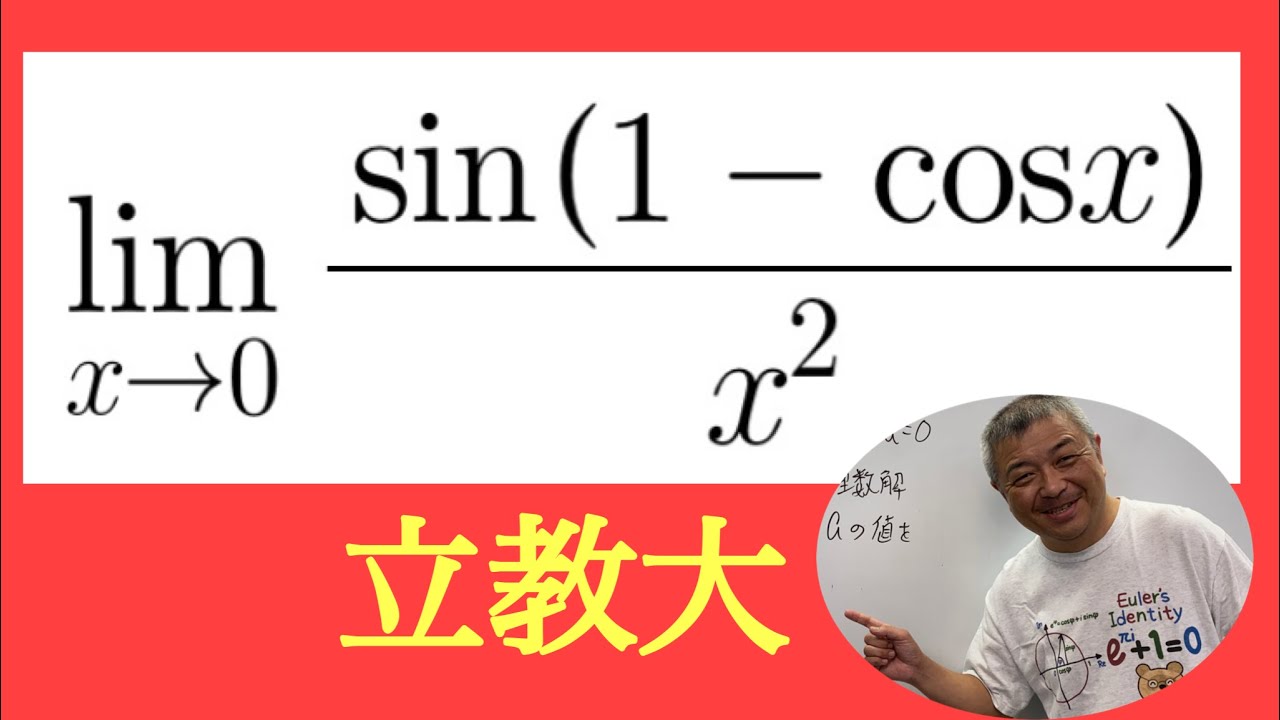問題文全文(内容文):
$\theta_n=([x]^n+[\displaystyle \frac{x}{n}])^{\frac{1}{n}}\pi$
(1)
$\displaystyle \lim_{ x \to \infty }\cos\theta_1$
(2)
$\displaystyle \lim_{ x \to \infty }\tan\theta_2$
$\theta_n=([x]^n+[\displaystyle \frac{x}{n}])^{\frac{1}{n}}\pi$
(1)
$\displaystyle \lim_{ x \to \infty }\cos\theta_1$
(2)
$\displaystyle \lim_{ x \to \infty }\tan\theta_2$
チャプター:
00:00 問題紹介
00:29 本編スタート (1) lim cos の解説
01:45 (2) lim tan の解説
07:48 作成した解答① lim cos
08:01 作成した解答② lim tan
08:12 作成した解答③
08:23 エンディング (音源提供 兄いえてぃ)
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\theta_n=([x]^n+[\displaystyle \frac{x}{n}])^{\frac{1}{n}}\pi$
(1)
$\displaystyle \lim_{ x \to \infty }\cos\theta_1$
(2)
$\displaystyle \lim_{ x \to \infty }\tan\theta_2$
$\theta_n=([x]^n+[\displaystyle \frac{x}{n}])^{\frac{1}{n}}\pi$
(1)
$\displaystyle \lim_{ x \to \infty }\cos\theta_1$
(2)
$\displaystyle \lim_{ x \to \infty }\tan\theta_2$
投稿日:2022.10.02