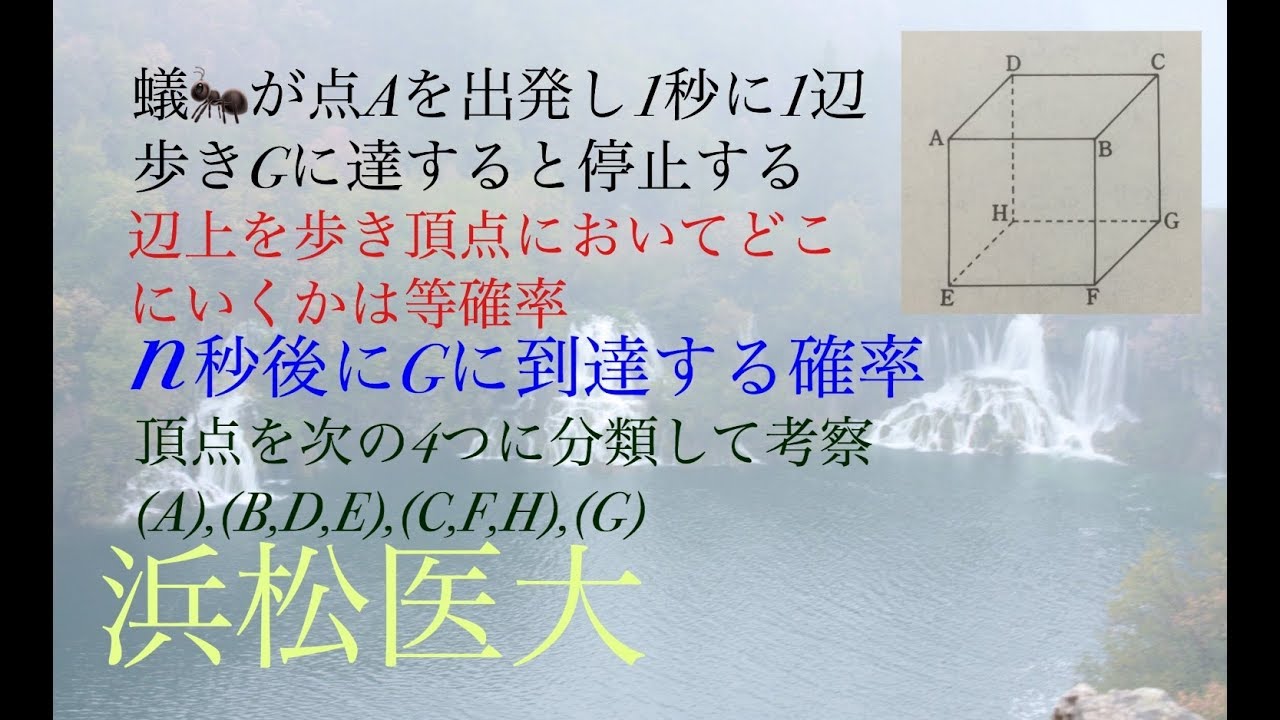
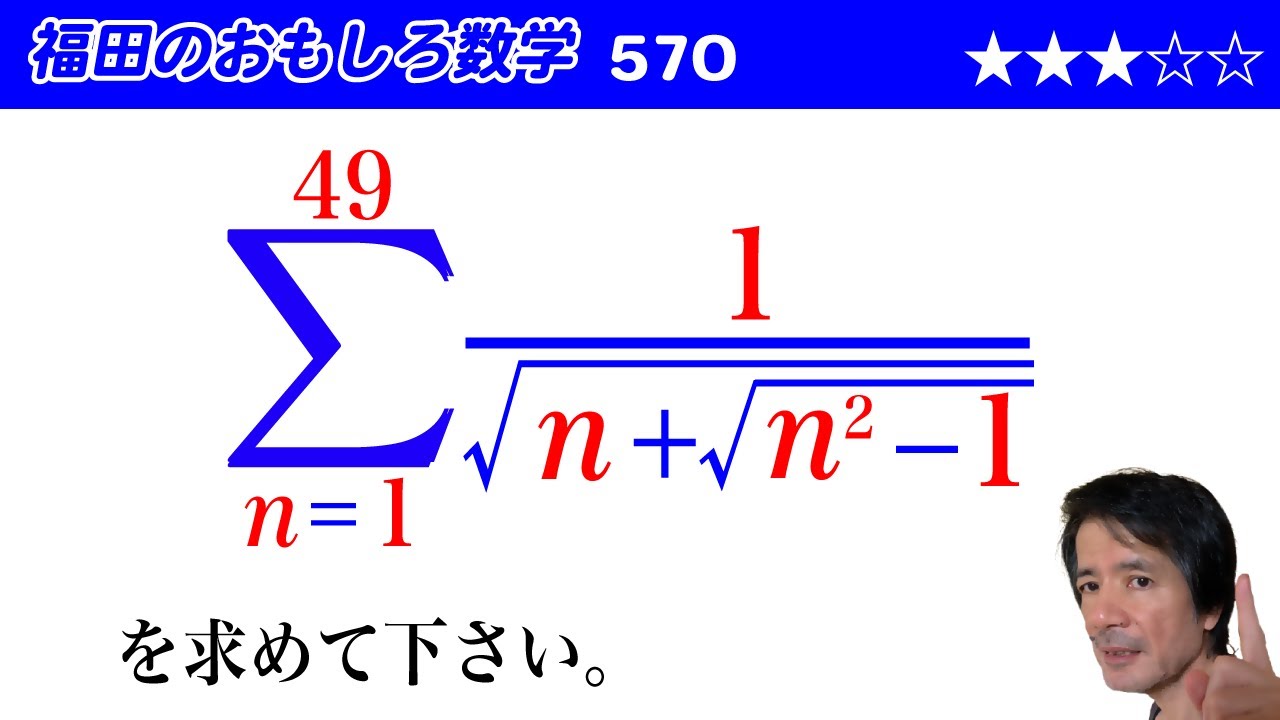
問題文全文(内容文):
一般項${an}$を出す公式
【等差】$a_{n}=$①____
【等比】$a_{n}=$②____
【階差】$(a_{n+1} -a_{n}=b_{n})$
③____のとき
$a_{n}=$④____________
◎グループ分けをしよう!
$\boxed{ A } a_{n+1} =2a_{n}$
$\boxed{ B } a_{n+1}-a_{n} =3^{n}$
$\boxed{ C } a_{n+1}+5a_{n} =0$
$\boxed{ D } a_{n+1}=a_{n}+7$
$\boxed{ E } a_{n+1}-3a_{n}=4$
$\boxed{ F } a_{n+1}-a_{n}=-2n+1$
等差数列は⑤____,等比数列は⑥____
階差数列は⑦____, 変形が必要なのは⑧____
⑧を変形すると⑨________ になる。
一般項${an}$を出す公式
【等差】$a_{n}=$①____
【等比】$a_{n}=$②____
【階差】$(a_{n+1} -a_{n}=b_{n})$
③____のとき
$a_{n}=$④____________
◎グループ分けをしよう!
$\boxed{ A } a_{n+1} =2a_{n}$
$\boxed{ B } a_{n+1}-a_{n} =3^{n}$
$\boxed{ C } a_{n+1}+5a_{n} =0$
$\boxed{ D } a_{n+1}=a_{n}+7$
$\boxed{ E } a_{n+1}-3a_{n}=4$
$\boxed{ F } a_{n+1}-a_{n}=-2n+1$
等差数列は⑤____,等比数列は⑥____
階差数列は⑦____, 変形が必要なのは⑧____
⑧を変形すると⑨________ になる。
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
一般項${an}$を出す公式
【等差】$a_{n}=$①____
【等比】$a_{n}=$②____
【階差】$(a_{n+1} -a_{n}=b_{n})$
③____のとき
$a_{n}=$④____________
◎グループ分けをしよう!
$\boxed{ A } a_{n+1} =2a_{n}$
$\boxed{ B } a_{n+1}-a_{n} =3^{n}$
$\boxed{ C } a_{n+1}+5a_{n} =0$
$\boxed{ D } a_{n+1}=a_{n}+7$
$\boxed{ E } a_{n+1}-3a_{n}=4$
$\boxed{ F } a_{n+1}-a_{n}=-2n+1$
等差数列は⑤____,等比数列は⑥____
階差数列は⑦____, 変形が必要なのは⑧____
⑧を変形すると⑨________ になる。
一般項${an}$を出す公式
【等差】$a_{n}=$①____
【等比】$a_{n}=$②____
【階差】$(a_{n+1} -a_{n}=b_{n})$
③____のとき
$a_{n}=$④____________
◎グループ分けをしよう!
$\boxed{ A } a_{n+1} =2a_{n}$
$\boxed{ B } a_{n+1}-a_{n} =3^{n}$
$\boxed{ C } a_{n+1}+5a_{n} =0$
$\boxed{ D } a_{n+1}=a_{n}+7$
$\boxed{ E } a_{n+1}-3a_{n}=4$
$\boxed{ F } a_{n+1}-a_{n}=-2n+1$
等差数列は⑤____,等比数列は⑥____
階差数列は⑦____, 変形が必要なのは⑧____
⑧を変形すると⑨________ になる。
投稿日:2013.05.27