【数学】中2-50 鋭角三角形と鈍角三角形 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 三角形と四角形 > 【数学】中2-50 鋭角三角形と鈍角三角形

【数学】中2-50 鋭角三角形と鈍角三角形

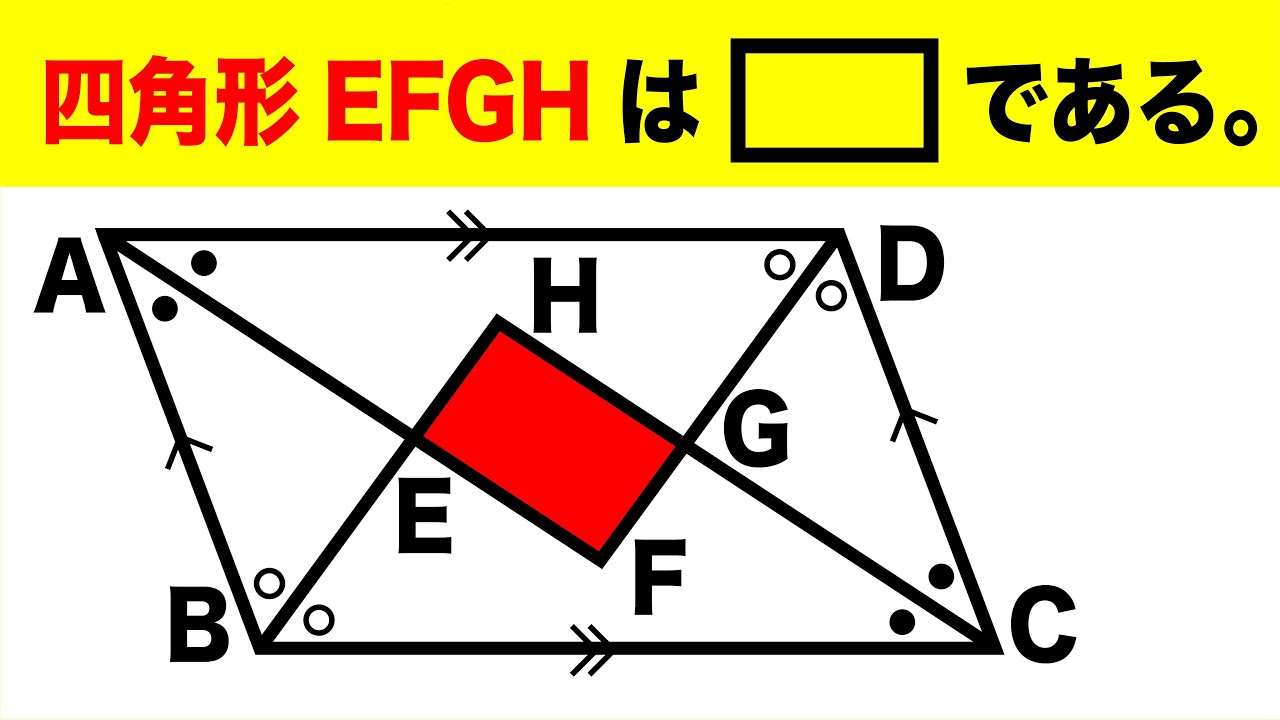
問題文全文(内容文)：
0°から90°の角を①＿＿＿＿、90°の角を②＿＿＿＿、90°から180°の角を③＿＿＿＿という。
①＿＿＿＿三角形は『④＿＿＿＿つの内角が⑤＿＿＿＿である三角形』、②＿＿＿＿三角形は『⑥＿＿つの内角が⑦＿＿である三角形』、③＿＿＿＿三角形は『⑧＿＿つの内角が⑨＿＿である三角形』！！

◎2つの内角が次の大きさのとき、どの三角形になる？
⑩32°、78°
⑪15°、123°
⑫35°、24°
⑬51°、39°

単元： #数学(中学生)#中２数学#三角形と四角形
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
0°から90°の角を①＿＿＿＿、90°の角を②＿＿＿＿、90°から180°の角を③＿＿＿＿という。
①＿＿＿＿三角形は『④＿＿＿＿つの内角が⑤＿＿＿＿である三角形』、②＿＿＿＿三角形は『⑥＿＿つの内角が⑦＿＿である三角形』、③＿＿＿＿三角形は『⑧＿＿つの内角が⑨＿＿である三角形』！！

◎2つの内角が次の大きさのとき、どの三角形になる？
⑩32°、78°
⑪15°、123°
⑫35°、24°
⑬51°、39°

投稿日：2013.10.30

＜関連動画＞

おうぎ形と三角形の面積は求め方が同じ？？

アイキャッチ画像
単元： #数学(中学生)#中２数学#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
面積は？
＊図は動画内参照
この動画を見る　

【条件をフル活用…！】図形：兵庫県公立高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中２数学#三角形と四角形#高校入試過去問(数学)#兵庫県公立高等学校
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.

兵庫県公立高等学校過去問
この動画を見る　

割り算

アイキャッチ画像
単元： #数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）
指導講師： 数学を数楽に
問題文全文(内容文)：
$3\div7=??$
$2024\div2025=??$
$2y\div3x=??$
この動画を見る　

一次関数であるものを選べ　　愛知県

アイキャッチ画像
単元： #数学(中学生)#中２数学#1次関数#高校入試過去問(数学)#愛知県公立高校入試
指導講師： 数学を数楽に
問題文全文(内容文)：
$yがxの1次関数となるものを選べ。$
ア 面積100cm$^2$でたての長さが$x$cmである長方形の横の長さ$y$cm
イ 1辺の長さ$x$cmである正三角形の周の長さ$y$cm
ウ 半径が$x$cmである円の面積$y$cm$^2$
エ 1辺の長さが$x$cmである立方体の体積$y$cm$^3$
この動画を見る　

正三角形の折り返し

アイキャッチ画像
単元： #数学(中学生)#中２数学#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
x=?
この動画を見る　
PAGE TOP