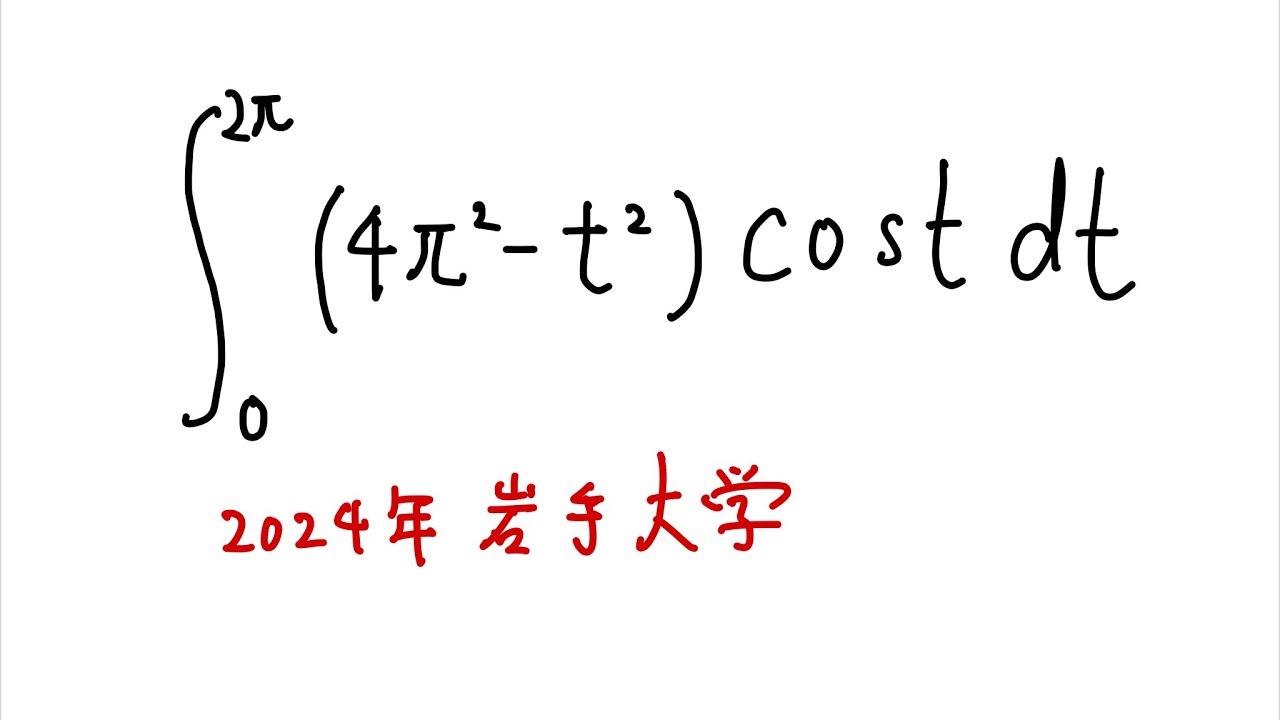問題文全文(内容文):
数Ⅲ(定積分と不等式の証明)
①$0≦x≦1$のとき、$1-x^2≦1-x^4≦1$が成り立つことを示せ。
②不等式$\frac{\pi}{4} \lt \int_0^1\sqrt{1-x^4}dx \lt 1$を示せ。
数Ⅲ(定積分と不等式の証明)
①$0≦x≦1$のとき、$1-x^2≦1-x^4≦1$が成り立つことを示せ。
②不等式$\frac{\pi}{4} \lt \int_0^1\sqrt{1-x^4}dx \lt 1$を示せ。
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(定積分と不等式の証明)
①$0≦x≦1$のとき、$1-x^2≦1-x^4≦1$が成り立つことを示せ。
②不等式$\frac{\pi}{4} \lt \int_0^1\sqrt{1-x^4}dx \lt 1$を示せ。
数Ⅲ(定積分と不等式の証明)
①$0≦x≦1$のとき、$1-x^2≦1-x^4≦1$が成り立つことを示せ。
②不等式$\frac{\pi}{4} \lt \int_0^1\sqrt{1-x^4}dx \lt 1$を示せ。
投稿日:2020.08.08