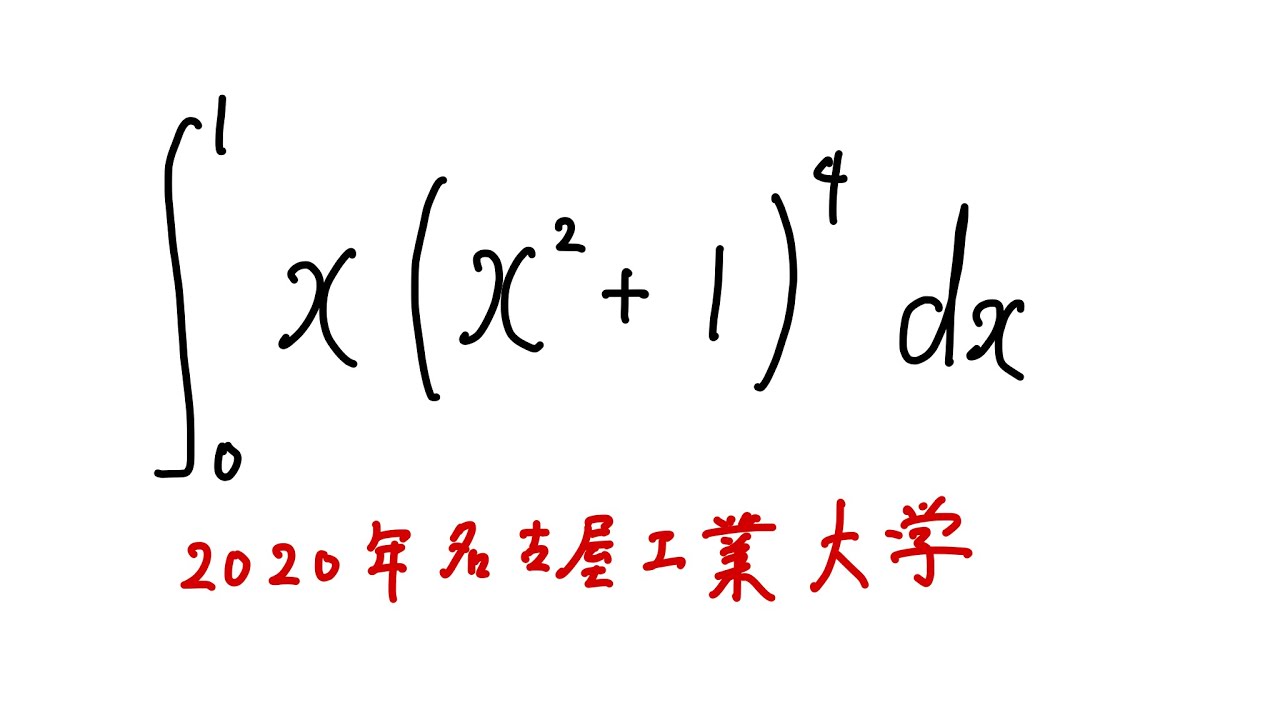http://youtu.be 問題文全文(内容文)：
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
投稿日：2022.05.24
