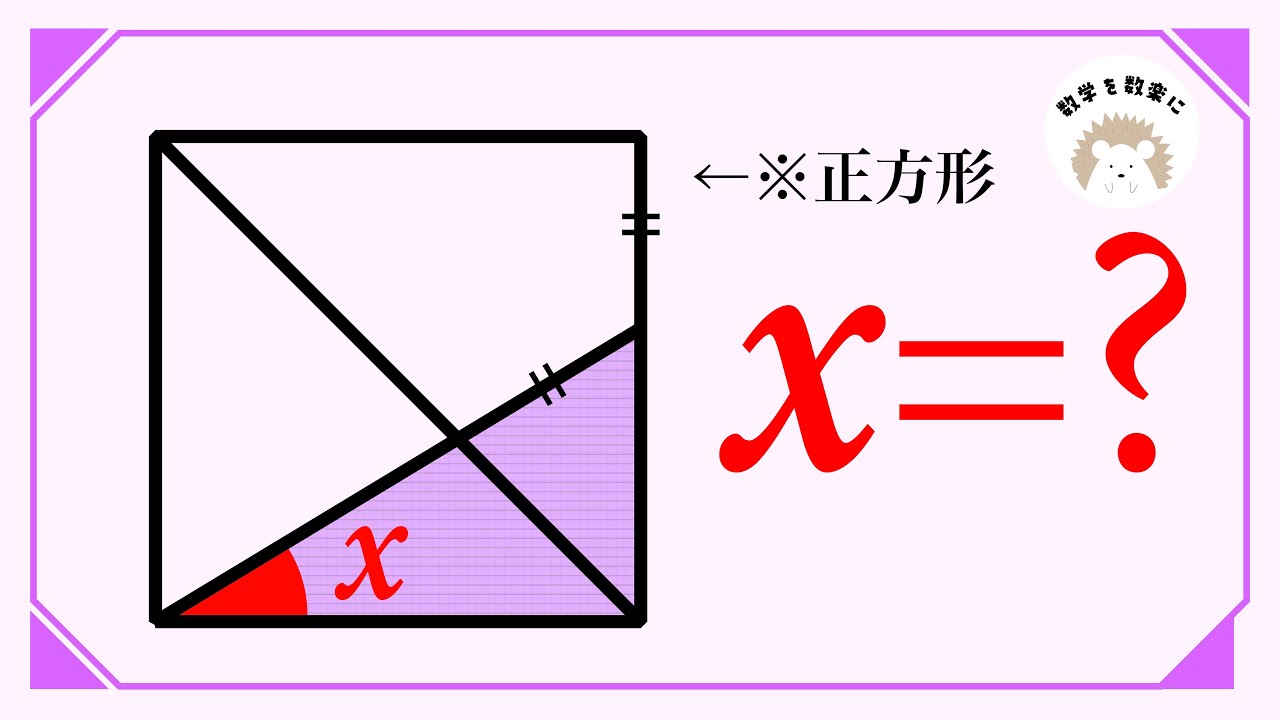
問題文全文(内容文):
右の図のように,線分$AB$を直径とする円$O$の円周上に,点$C$をとります.
円$O$と,$CO$の延長との交点を$D$とし,
点$C$を通る円$O$の接線と$\angle BOC$の二等分線との交点を$E$とします.
このとき,次の問いに答えなさい.
①$OB=4cm, \angle BOD = 120°$のとき,
線分$BD$の長さを求めなさい.
②$△ABC ∞ OEC$を証明しなさい.
図は動画内参照
右の図のように,線分$AB$を直径とする円$O$の円周上に,点$C$をとります.
円$O$と,$CO$の延長との交点を$D$とし,
点$C$を通る円$O$の接線と$\angle BOC$の二等分線との交点を$E$とします.
このとき,次の問いに答えなさい.
①$OB=4cm, \angle BOD = 120°$のとき,
線分$BD$の長さを求めなさい.
②$△ABC ∞ OEC$を証明しなさい.
図は動画内参照
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように,線分$AB$を直径とする円$O$の円周上に,点$C$をとります.
円$O$と,$CO$の延長との交点を$D$とし,
点$C$を通る円$O$の接線と$\angle BOC$の二等分線との交点を$E$とします.
このとき,次の問いに答えなさい.
①$OB=4cm, \angle BOD = 120°$のとき,
線分$BD$の長さを求めなさい.
②$△ABC ∞ OEC$を証明しなさい.
図は動画内参照
右の図のように,線分$AB$を直径とする円$O$の円周上に,点$C$をとります.
円$O$と,$CO$の延長との交点を$D$とし,
点$C$を通る円$O$の接線と$\angle BOC$の二等分線との交点を$E$とします.
このとき,次の問いに答えなさい.
①$OB=4cm, \angle BOD = 120°$のとき,
線分$BD$の長さを求めなさい.
②$△ABC ∞ OEC$を証明しなさい.
図は動画内参照
投稿日:2017.01.26