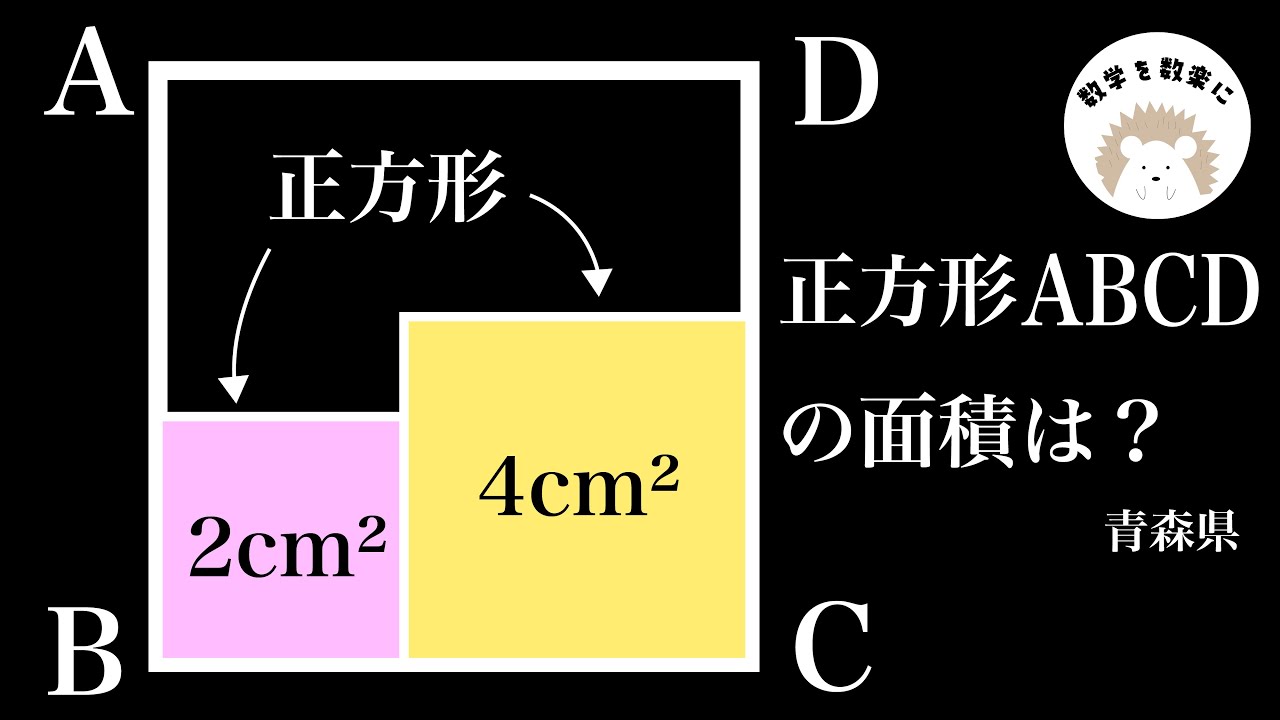
問題文全文(内容文):
$x= \frac{3 + \sqrt {11}}{2}$ , $y= \frac{3- \sqrt{11}}{2}$
$\frac{x^4-y^4}{12} =?$
大阪星光学院高等学校
$x= \frac{3 + \sqrt {11}}{2}$ , $y= \frac{3- \sqrt{11}}{2}$
$\frac{x^4-y^4}{12} =?$
大阪星光学院高等学校
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x= \frac{3 + \sqrt {11}}{2}$ , $y= \frac{3- \sqrt{11}}{2}$
$\frac{x^4-y^4}{12} =?$
大阪星光学院高等学校
$x= \frac{3 + \sqrt {11}}{2}$ , $y= \frac{3- \sqrt{11}}{2}$
$\frac{x^4-y^4}{12} =?$
大阪星光学院高等学校
投稿日:2022.05.17