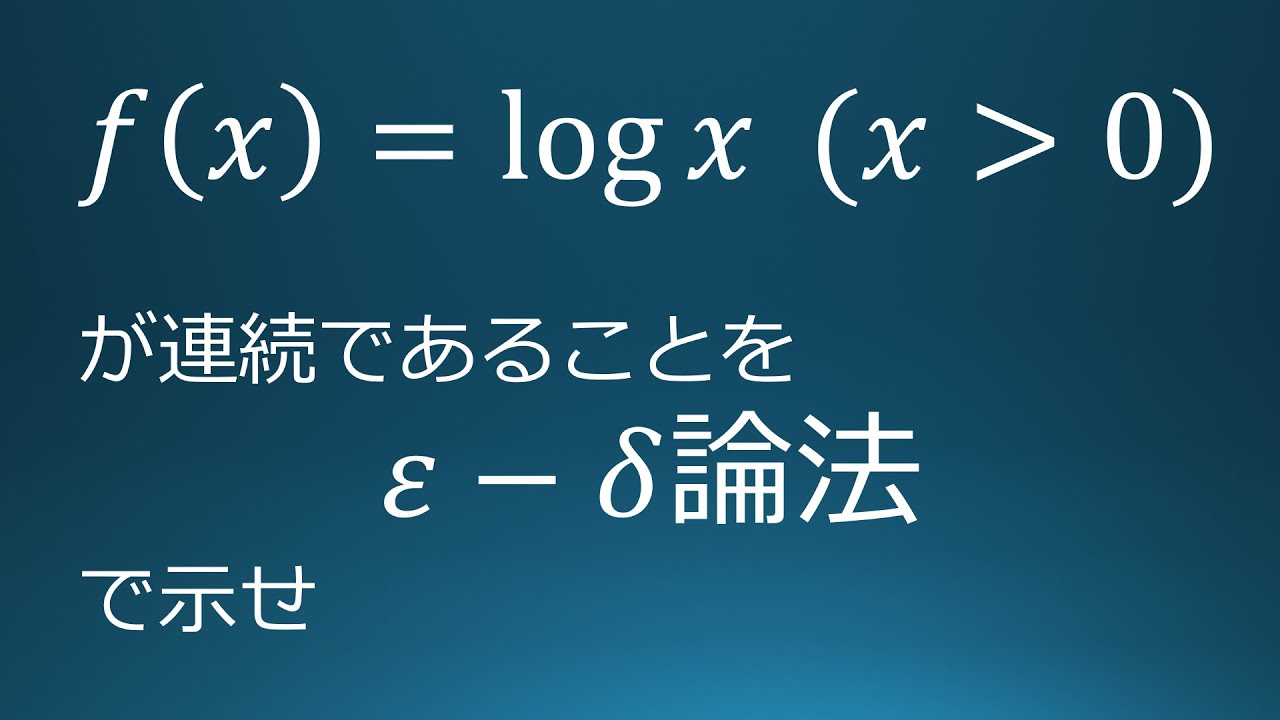【数学II】二項定理

問題文全文(内容文)：
【数学II】二項定理　解説動画です

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：カサニマロ【べんとう・ふきのとうの授業動画】

問題文全文(内容文)：
【数学II】二項定理　解説動画です

投稿日：2019.05.05

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$x$は自然数とする.
整式$x^n$を整式$x^2-2x-1$ｓｗ割った余りを$ax+b$とする.
$a,b$は整数であり,$a,b$をともに割り切る素数は無いことを示せ.

2013京都大過去問

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
どっちがでかい？
$1.11^{111}\ vs\ 1111$

この動画を見る　

単元： #数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\dfrac {y+z}{b-c}=\dfrac{z+x}{c-a}=\dfrac{x+y}{a-b}$ のとき、
$x+y+z=0$ であることを証明せよ。

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#その他#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$\boxed{3}$ $x^9-3x^8$を$x^2+x+1$で割った余りを求めよ.

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：

$\begin{eqnarray}
1+\frac{1}{1+\frac{1}{1+\frac{1}{1+n}}}
\end{eqnarray}$

は整数になれない。証明して下さい。

＊$n$は整数である。

この動画を見る　