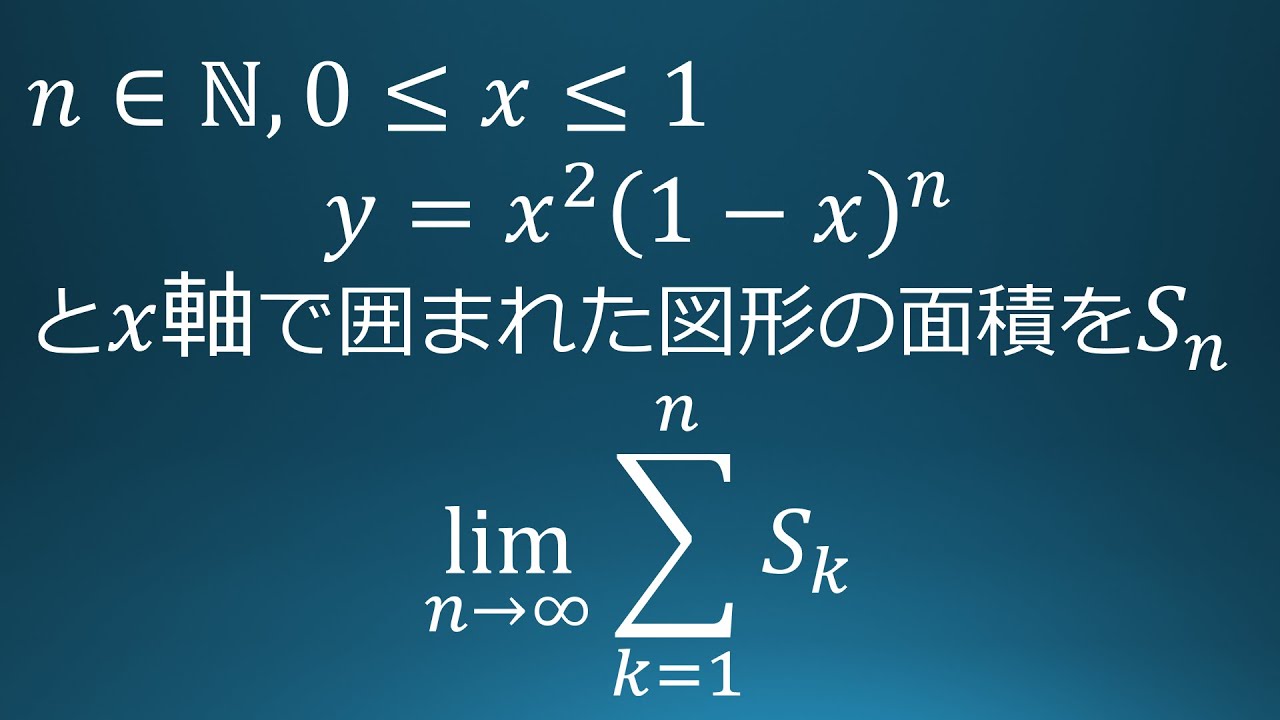問題文全文(内容文):
$ \displaystyle \lim_{(x,y)\to (0,0)}\dfrac{x^2-y^2}{x^2+y^2}$
次の関数の極限を調べよ.
$ \displaystyle \lim_{(x,y)\to (0,0)}\dfrac{x^2-y^2}{x^2+y^2}$
次の関数の極限を調べよ.
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{(x,y)\to (0,0)}\dfrac{x^2-y^2}{x^2+y^2}$
次の関数の極限を調べよ.
$ \displaystyle \lim_{(x,y)\to (0,0)}\dfrac{x^2-y^2}{x^2+y^2}$
次の関数の極限を調べよ.
投稿日:2024.01.07