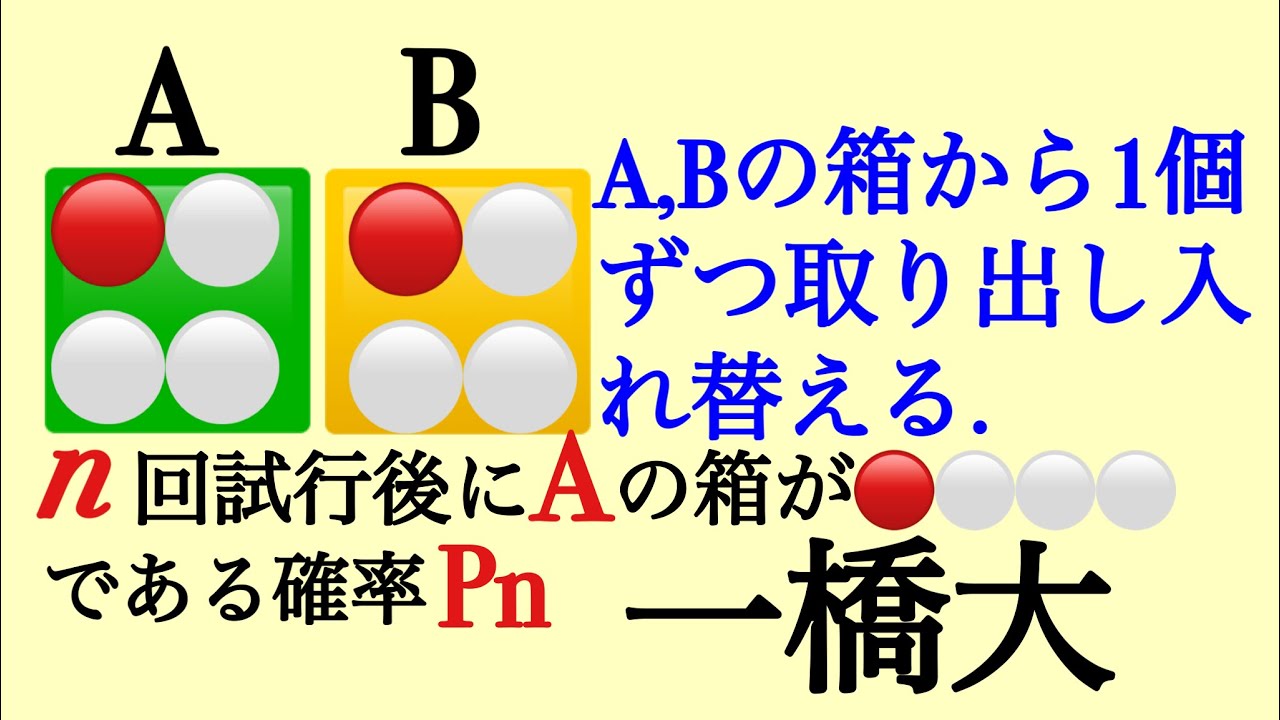
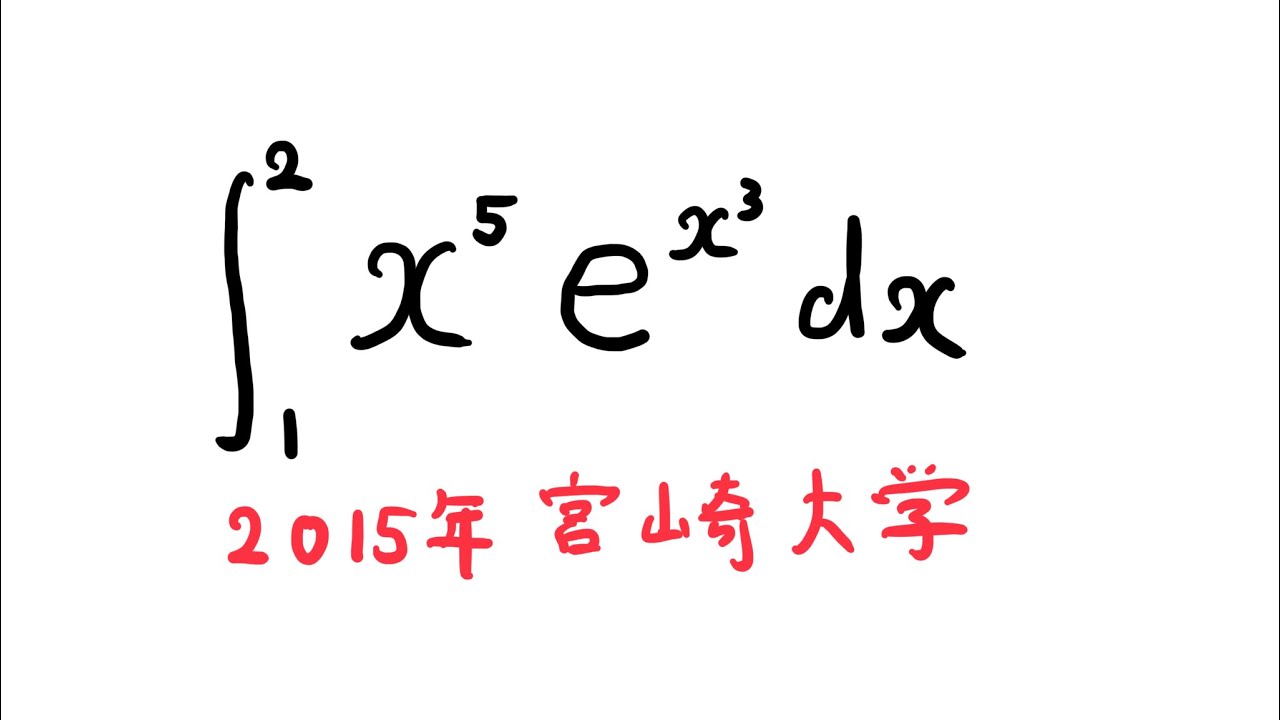問題文全文(内容文):
${\large\boxed{6}}$まず、1期目の交渉案の分配値が$\textrm{A}$と$\textrm{B}$共に紛争で期待できる価値以上であれば、交渉案を受け入れ紛争を起こさず、期待できる価値未満であれば紛争を起こすものとすると、$\textrm{A}$は自らの分配値が$\displaystyle\frac{\boxed{ア}}{35}$以上であれば交渉案を受け入れ、$\textrm{B}$は$\textrm{A}$の分配値が1以下であれば交渉権を受け入れる。また紛争が起きた場合には、2期目と3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は1期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし1期目に交渉が妥結した場合は、2期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{イ}}{35}$以上で$\displaystyle\frac{\boxed{ウ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なので$\textrm{A}$と$\textrm{B}$ともに交渉案を受け入れ紛争を起こさず、そうでない場合には紛争を起こし、その場合には3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は2期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし2期目に交渉が妥結した場合は、3期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{エ}}{35}$以上で$\displaystyle\frac{\boxed{オ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なの$\textrm{A}$と$\textrm{B}$共に交渉案を受け入れ紛争を起こさず、\begin{eqnarray}\end{eqnarray}
以下では、各期において交渉が妥結した場合には、$\textrm{A}$の分配値は$\textrm{A}$と$\textrm{B}$共に受け入れられる$\textrm{A}$の分配値の上限値と下限値の中間に定まるものと仮定しよう。すると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥協した場合$\displaystyle\frac{\boxed{カ}}{35}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{キ}}{35}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ク}}{35}$であり、3期目に紛争が起きた場合$\displaystyle\frac{\boxed{ケ}}{35}$となる。\begin{eqnarray}\end{eqnarray}
また、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加した場合、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{コ}}{70}$となり、1期目に紛争が起きた場合、$\displaystyle\frac{\boxed{サ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{シ}}{70}$となる。さらに、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加し、問題となっている土地の価値が2期と3期で$\textrm{A}$と$\textrm{A}$共に2に増加したとすると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{ス}}{70}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{セ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ソ}}{70}$となる。
2023慶應義塾大学総合政策学部過去問
${\large\boxed{6}}$まず、1期目の交渉案の分配値が$\textrm{A}$と$\textrm{B}$共に紛争で期待できる価値以上であれば、交渉案を受け入れ紛争を起こさず、期待できる価値未満であれば紛争を起こすものとすると、$\textrm{A}$は自らの分配値が$\displaystyle\frac{\boxed{ア}}{35}$以上であれば交渉案を受け入れ、$\textrm{B}$は$\textrm{A}$の分配値が1以下であれば交渉権を受け入れる。また紛争が起きた場合には、2期目と3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は1期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし1期目に交渉が妥結した場合は、2期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{イ}}{35}$以上で$\displaystyle\frac{\boxed{ウ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なので$\textrm{A}$と$\textrm{B}$ともに交渉案を受け入れ紛争を起こさず、そうでない場合には紛争を起こし、その場合には3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は2期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし2期目に交渉が妥結した場合は、3期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{エ}}{35}$以上で$\displaystyle\frac{\boxed{オ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なの$\textrm{A}$と$\textrm{B}$共に交渉案を受け入れ紛争を起こさず、\begin{eqnarray}\end{eqnarray}
以下では、各期において交渉が妥結した場合には、$\textrm{A}$の分配値は$\textrm{A}$と$\textrm{B}$共に受け入れられる$\textrm{A}$の分配値の上限値と下限値の中間に定まるものと仮定しよう。すると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥協した場合$\displaystyle\frac{\boxed{カ}}{35}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{キ}}{35}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ク}}{35}$であり、3期目に紛争が起きた場合$\displaystyle\frac{\boxed{ケ}}{35}$となる。\begin{eqnarray}\end{eqnarray}
また、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加した場合、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{コ}}{70}$となり、1期目に紛争が起きた場合、$\displaystyle\frac{\boxed{サ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{シ}}{70}$となる。さらに、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加し、問題となっている土地の価値が2期と3期で$\textrm{A}$と$\textrm{A}$共に2に増加したとすると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{ス}}{70}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{セ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ソ}}{70}$となる。
2023慶應義塾大学総合政策学部過去問
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$まず、1期目の交渉案の分配値が$\textrm{A}$と$\textrm{B}$共に紛争で期待できる価値以上であれば、交渉案を受け入れ紛争を起こさず、期待できる価値未満であれば紛争を起こすものとすると、$\textrm{A}$は自らの分配値が$\displaystyle\frac{\boxed{ア}}{35}$以上であれば交渉案を受け入れ、$\textrm{B}$は$\textrm{A}$の分配値が1以下であれば交渉権を受け入れる。また紛争が起きた場合には、2期目と3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は1期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし1期目に交渉が妥結した場合は、2期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{イ}}{35}$以上で$\displaystyle\frac{\boxed{ウ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なので$\textrm{A}$と$\textrm{B}$ともに交渉案を受け入れ紛争を起こさず、そうでない場合には紛争を起こし、その場合には3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は2期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし2期目に交渉が妥結した場合は、3期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{エ}}{35}$以上で$\displaystyle\frac{\boxed{オ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なの$\textrm{A}$と$\textrm{B}$共に交渉案を受け入れ紛争を起こさず、\begin{eqnarray}\end{eqnarray}
以下では、各期において交渉が妥結した場合には、$\textrm{A}$の分配値は$\textrm{A}$と$\textrm{B}$共に受け入れられる$\textrm{A}$の分配値の上限値と下限値の中間に定まるものと仮定しよう。すると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥協した場合$\displaystyle\frac{\boxed{カ}}{35}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{キ}}{35}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ク}}{35}$であり、3期目に紛争が起きた場合$\displaystyle\frac{\boxed{ケ}}{35}$となる。\begin{eqnarray}\end{eqnarray}
また、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加した場合、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{コ}}{70}$となり、1期目に紛争が起きた場合、$\displaystyle\frac{\boxed{サ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{シ}}{70}$となる。さらに、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加し、問題となっている土地の価値が2期と3期で$\textrm{A}$と$\textrm{A}$共に2に増加したとすると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{ス}}{70}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{セ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ソ}}{70}$となる。
2023慶應義塾大学総合政策学部過去問
${\large\boxed{6}}$まず、1期目の交渉案の分配値が$\textrm{A}$と$\textrm{B}$共に紛争で期待できる価値以上であれば、交渉案を受け入れ紛争を起こさず、期待できる価値未満であれば紛争を起こすものとすると、$\textrm{A}$は自らの分配値が$\displaystyle\frac{\boxed{ア}}{35}$以上であれば交渉案を受け入れ、$\textrm{B}$は$\textrm{A}$の分配値が1以下であれば交渉権を受け入れる。また紛争が起きた場合には、2期目と3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は1期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし1期目に交渉が妥結した場合は、2期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{イ}}{35}$以上で$\displaystyle\frac{\boxed{ウ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なので$\textrm{A}$と$\textrm{B}$ともに交渉案を受け入れ紛争を起こさず、そうでない場合には紛争を起こし、その場合には3期目に$\textrm{A}$と$\textrm{B}$が期待できる価値は2期目に期待できる価値と同一とする。\begin{eqnarray}\end{eqnarray}
もし2期目に交渉が妥結した場合は、3期目に改めて交渉が行われ、$\textrm{A}$の分配値が$\displaystyle\frac{\boxed{エ}}{35}$以上で$\displaystyle\frac{\boxed{オ}}{35}$以下ならば、$\textrm{A}$と$\textrm{B}$ともに紛争で期待できる価値以上なの$\textrm{A}$と$\textrm{B}$共に交渉案を受け入れ紛争を起こさず、\begin{eqnarray}\end{eqnarray}
以下では、各期において交渉が妥結した場合には、$\textrm{A}$の分配値は$\textrm{A}$と$\textrm{B}$共に受け入れられる$\textrm{A}$の分配値の上限値と下限値の中間に定まるものと仮定しよう。すると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥協した場合$\displaystyle\frac{\boxed{カ}}{35}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{キ}}{35}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ク}}{35}$であり、3期目に紛争が起きた場合$\displaystyle\frac{\boxed{ケ}}{35}$となる。\begin{eqnarray}\end{eqnarray}
また、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加した場合、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{コ}}{70}$となり、1期目に紛争が起きた場合、$\displaystyle\frac{\boxed{サ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{シ}}{70}$となる。さらに、紛争コストが$\textrm{A}$と$\textrm{B}$共に$\displaystyle\frac{2}{5}$に増加し、問題となっている土地の価値が2期と3期で$\textrm{A}$と$\textrm{A}$共に2に増加したとすると、$\textrm{A}$が得られると期待できる価値の3期分の合計は、3期すべてで交渉が妥結した場合$\displaystyle\frac{\boxed{ス}}{70}$となり、1期目に紛争が起きた場合$\displaystyle\frac{\boxed{セ}}{70}$であり、2期目に紛争が起きた場合$\displaystyle\frac{\boxed{ソ}}{70}$となる。
2023慶應義塾大学総合政策学部過去問
投稿日:2023.12.07