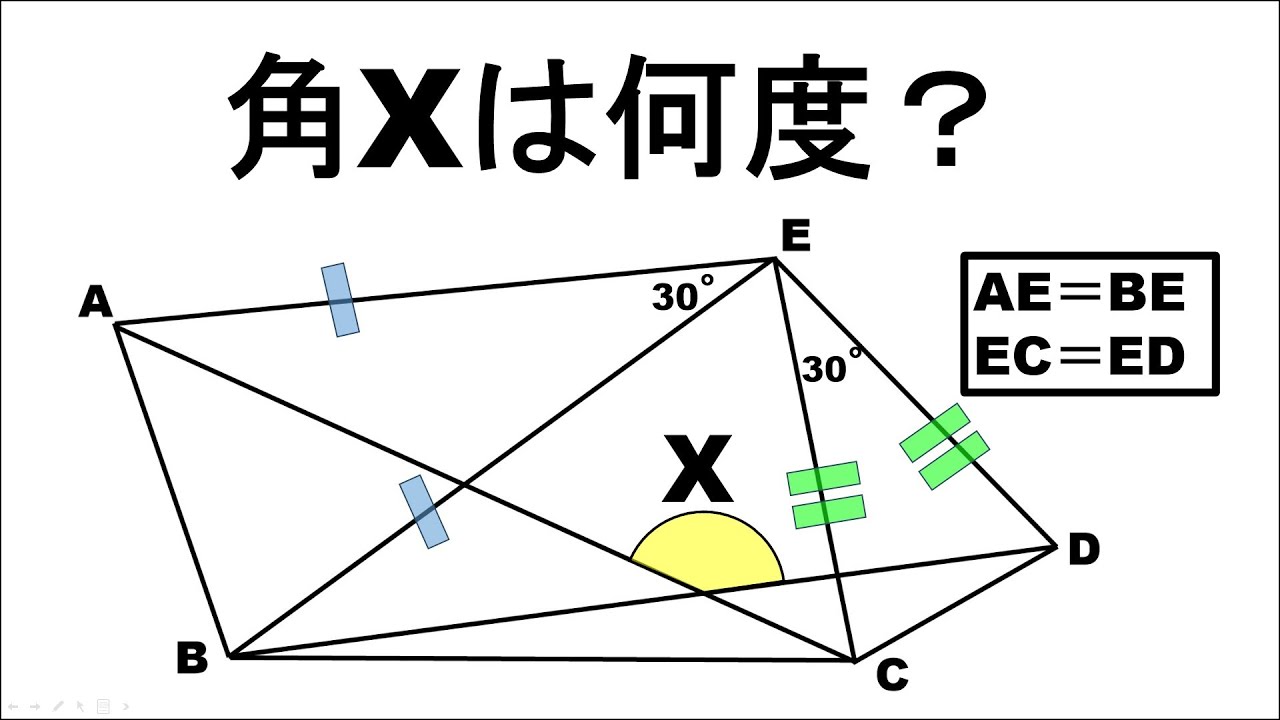
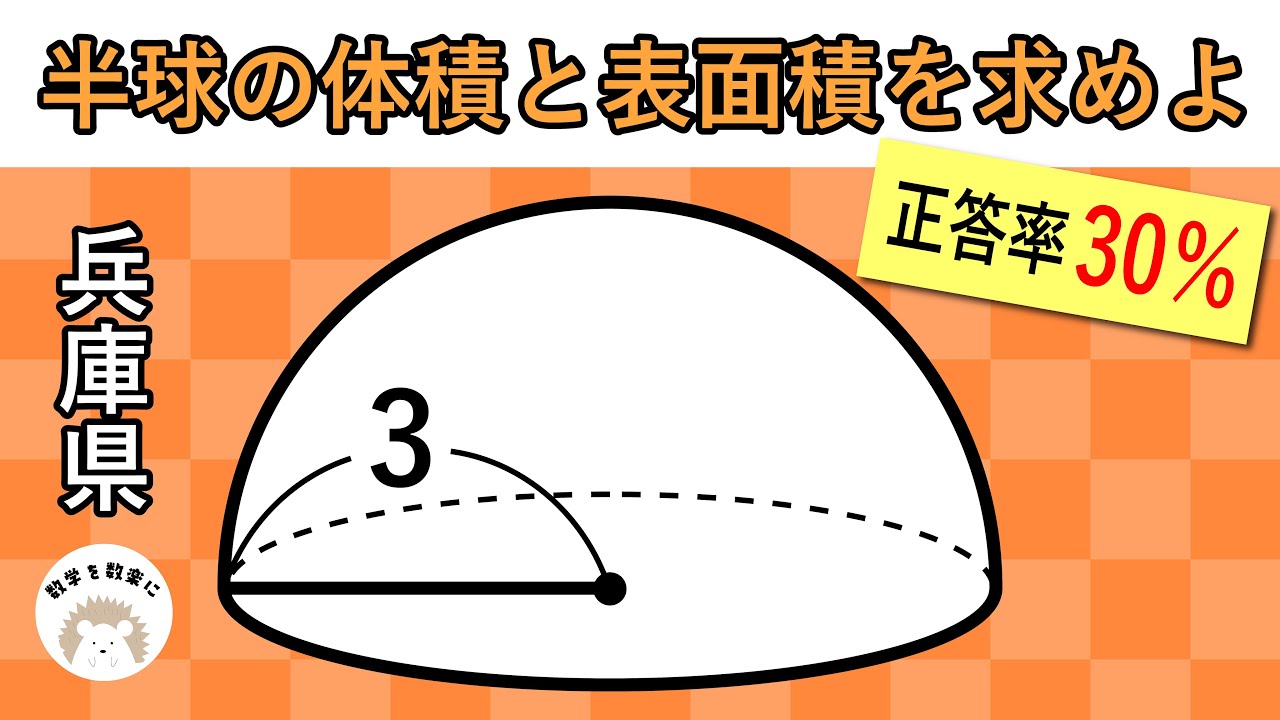
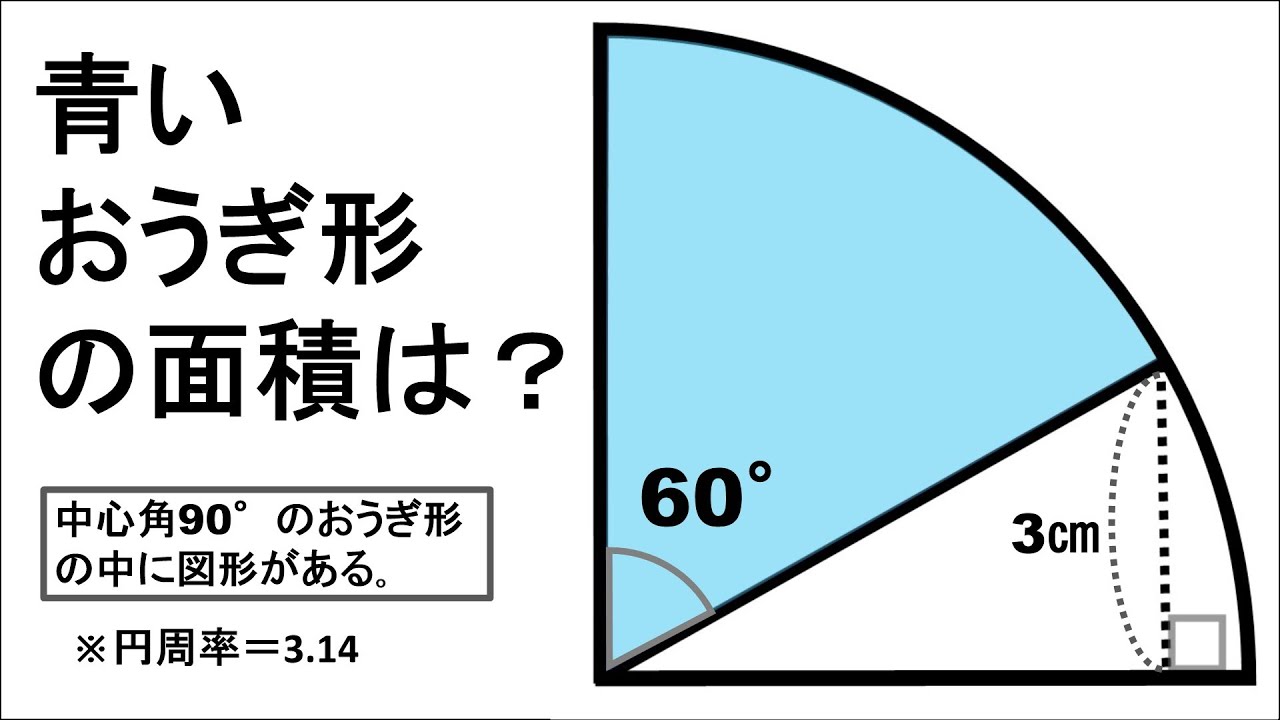
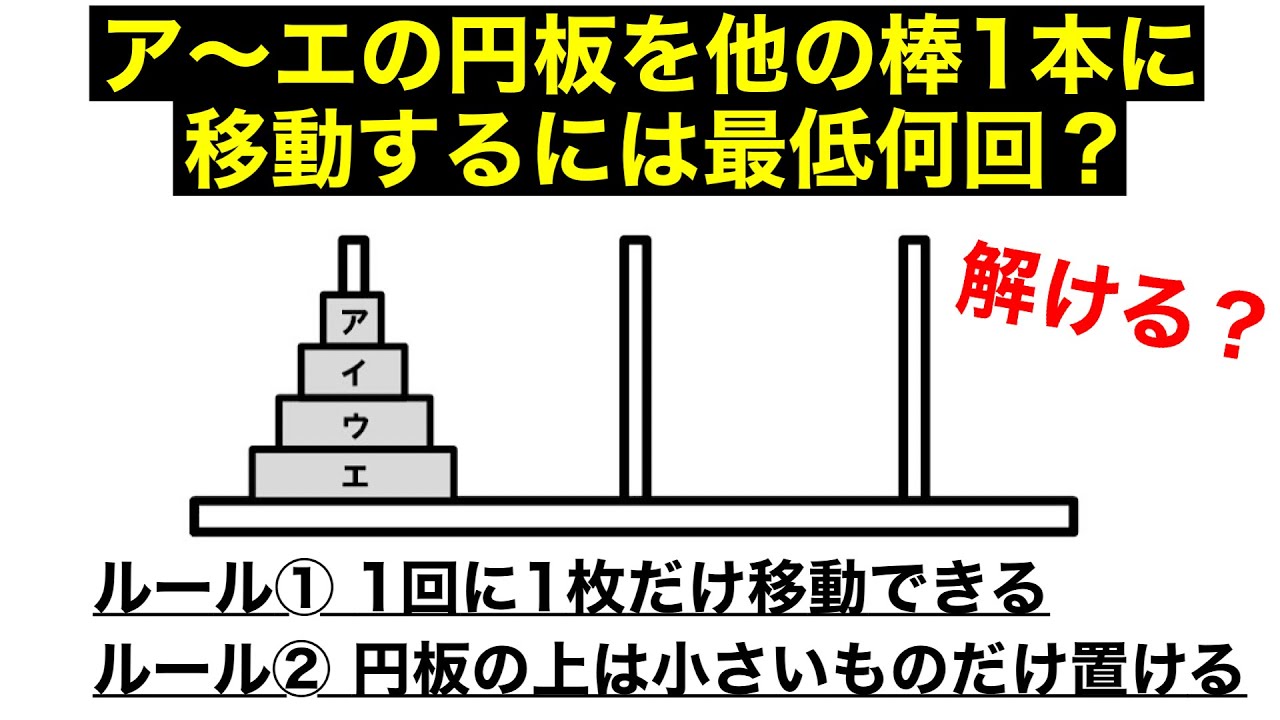
問題文全文(内容文):
第12回平均算②
例1
ひとみさんがこれまで受けた算数のテストの平均点が68点です。次のテストで100点をとると、平均点が72点になります。
ひとみさんはこれまでに何回テストを受けましたか?
例2
あるクラスで算数のテストをしました。男子22人の平均点は50点で、 女子の平均点は60点でした。
クラス全体の平均点が54.5点のとき クラスの人数は何人ですか。
第12回平均算②
例1
ひとみさんがこれまで受けた算数のテストの平均点が68点です。次のテストで100点をとると、平均点が72点になります。
ひとみさんはこれまでに何回テストを受けましたか?
例2
あるクラスで算数のテストをしました。男子22人の平均点は50点で、 女子の平均点は60点でした。
クラス全体の平均点が54.5点のとき クラスの人数は何人ですか。
単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第12回平均算②
例1
ひとみさんがこれまで受けた算数のテストの平均点が68点です。次のテストで100点をとると、平均点が72点になります。
ひとみさんはこれまでに何回テストを受けましたか?
例2
あるクラスで算数のテストをしました。男子22人の平均点は50点で、 女子の平均点は60点でした。
クラス全体の平均点が54.5点のとき クラスの人数は何人ですか。
第12回平均算②
例1
ひとみさんがこれまで受けた算数のテストの平均点が68点です。次のテストで100点をとると、平均点が72点になります。
ひとみさんはこれまでに何回テストを受けましたか?
例2
あるクラスで算数のテストをしました。男子22人の平均点は50点で、 女子の平均点は60点でした。
クラス全体の平均点が54.5点のとき クラスの人数は何人ですか。
投稿日:2020.03.30