【中学数学】平方根：√2=1.414を使って近似値を求めよう！根号の変形方法は？

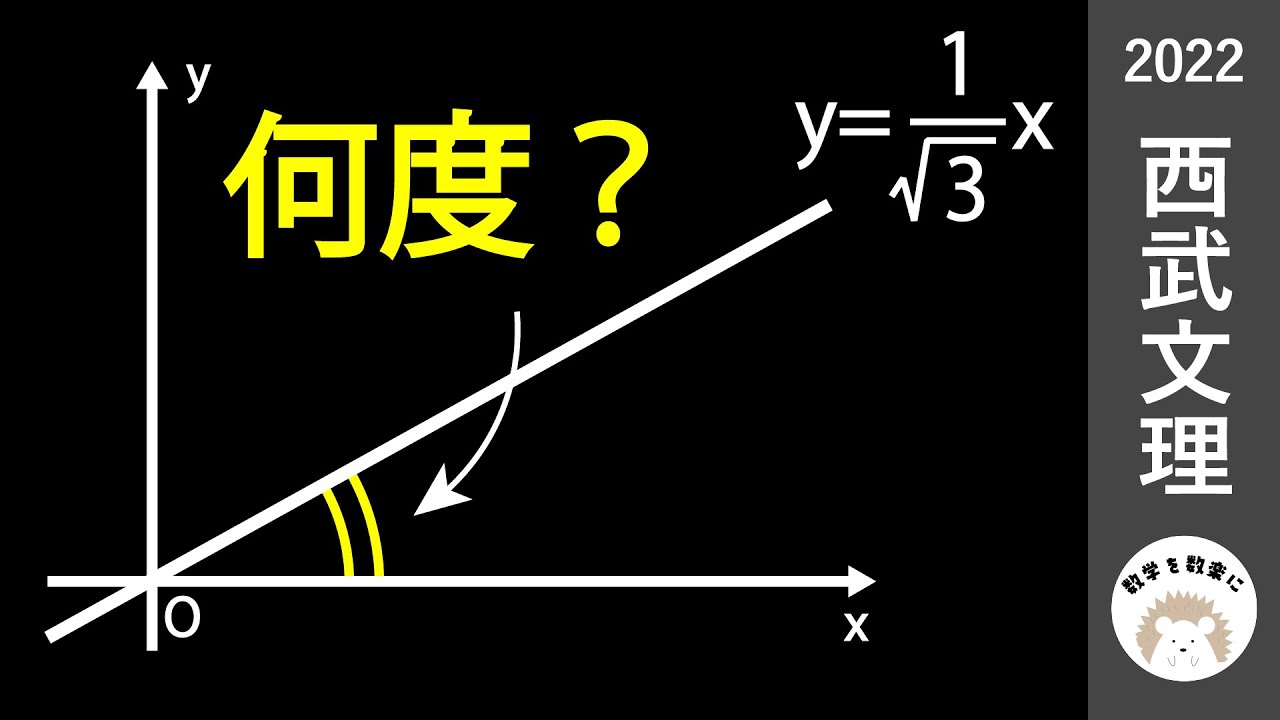
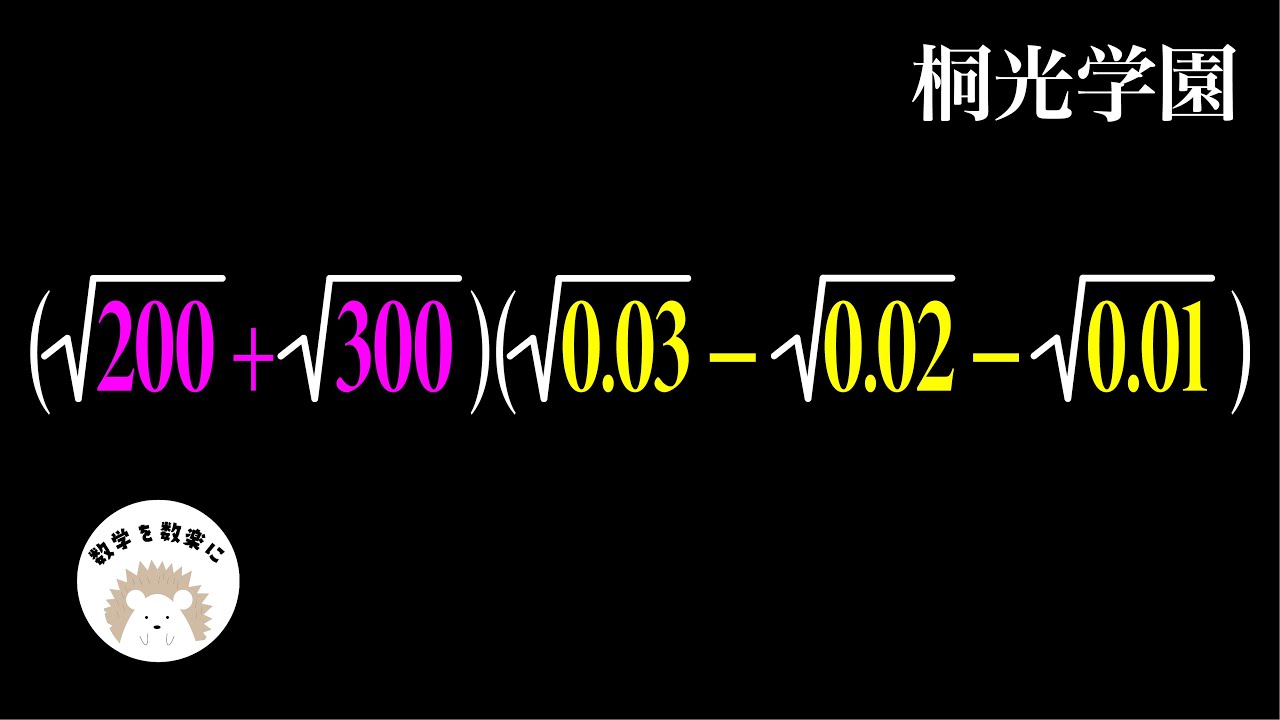問題文全文(内容文)：
$\sqrt2=1.414$のとき、次の値を求めよ。
(1)$\sqrt{50}$
(2)$\sqrt{18}$
(3)$\sqrt{200}$
(4)$\sqrt{20000}$
(5)$\sqrt{0.02}$

チャプター：

0:00 オープニング
0:04 (1)√50
1:03 (2)√18
1:44 (3)√200
2:22 (4)√20000
3:07 (5)√0.02

単元： #数学(中学生)#中３数学#平方根

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\sqrt2=1.414$のとき、次の値を求めよ。
(1)$\sqrt{50}$
(2)$\sqrt{18}$
(3)$\sqrt{200}$
(4)$\sqrt{20000}$
(5)$\sqrt{0.02}$

投稿日：2020.06.05

単元： #数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$

2⃣
$x^2+2xy+y^2$

この動画を見る　

単元： #数学(中学生)#中３数学#平方根#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
平方根（有理数と無理数）に関して解説していきます.

この動画を見る　

単元： #数学(中学生)#中３数学#平方根#高校入試過去問(数学)#中央大学附属高等学校

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
$ (\sqrt5+\sqrt3)^2-\sqrt2(\sqrt{10}+\sqrt6)\times (\sqrt5-\sqrt3)+(\sqrt5-\sqrt3)^2 $
を計算しなさい.

中央大附属高校過去問

この動画を見る　

単元： #数学(中学生)#中３数学#平方根

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
π<n<√50を満たす整数nをすべて求めよ。

この動画を見る　

単元： #数学(中学生)#中３数学#平方根

指導講師：数学を数楽に

問題文全文(内容文)：
$sqrt{x}$

この動画を見る　