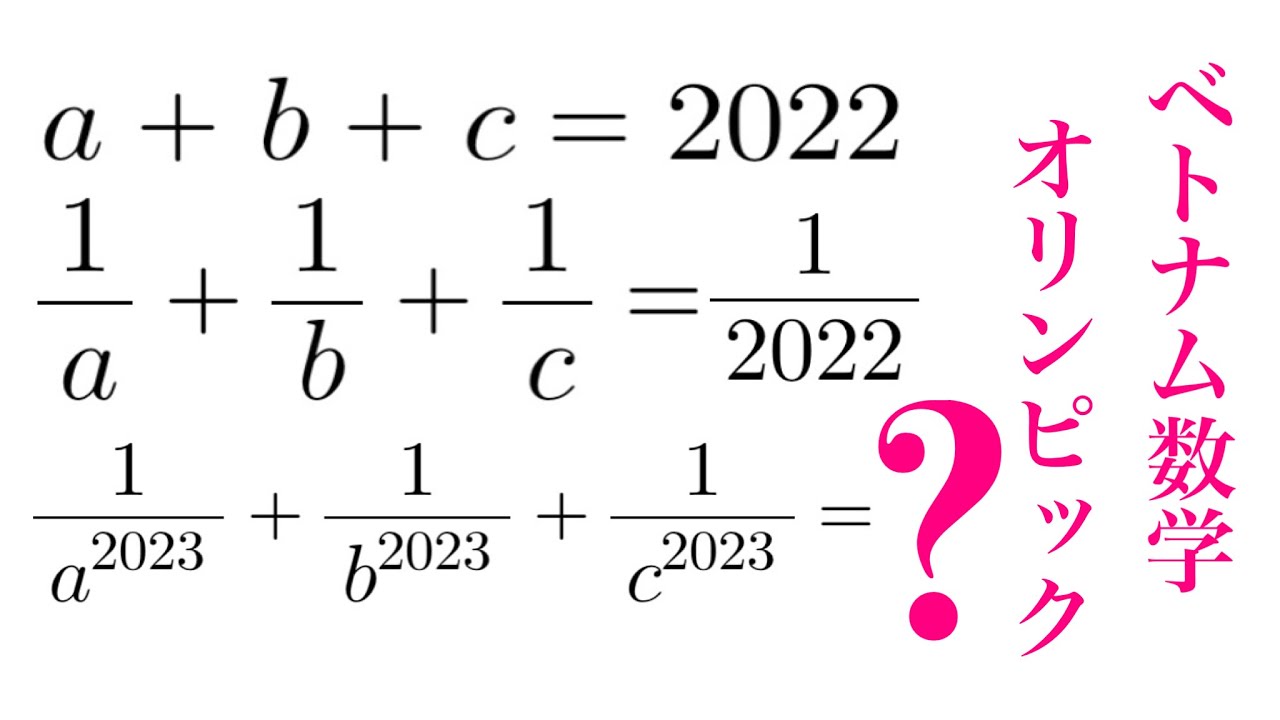2022乗 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅱ > 指数関数と対数関数 > 指数関数 > 2022乗

2022乗

問題文全文(内容文)：
$(5+2 \sqrt 6)^{1011}(\sqrt 3 - \sqrt 2)^{2022}$
単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
$(5+2 \sqrt 6)^{1011}(\sqrt 3 - \sqrt 2)^{2022}$
投稿日：2022.06.22

＜関連動画＞

【数Ⅱ】【指数関数と対数関数】指数対数計算5 ※問題文は概要欄

アイキャッチ画像
単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材： #4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#指数関数と対数関数#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
次の式の値を求めよ。
(1) $5^{\log_{5} 7}$
(2) $10^{1+\log_{10} 3}$
(3) $36^{\log_6 \sqrt{5}}$
(4) $7^{\log_{49} 4}$

$xyz≠0$, $2^x=5^y=10^{\frac{2}{z}}$のとき、等式$\frac{1}{x}+\frac{1}{y}=\frac{2}{z}$を証明せよ。

$\log_{11} 2$の小数第1位の数を求めよ。
この動画を見る　

指数

アイキャッチ画像
単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$3^x-5^y=3375$のとき,$\dfrac{xy}{x+y}$の値を求めよ.
この動画を見る　

【数Ⅱ】指数関数・対数関数：大小比較①　次の各組の数の大小を不等号を用いて表せ。(1)2の1/2乗,　4の1/4乗,　8の1/8乗

アイキャッチ画像
単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材： #チャート式#青チャートⅡ・B#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
次の各組の数の大小を不等号を用いて表せ。
(1)$2$の$\dfrac{1}{2}$乗,$4$の$\dfrac{1}{4}$乗,$8$の$\dfrac{1}{8}$乗
この動画を見る　

慶応義塾大　指数方程式

アイキャッチ画像
単元： #数Ⅱ#指数関数と対数関数#微分法と積分法#指数関数#微分とその応用#数学(高校生)#数Ⅲ
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$8^x-6・4^x+5・2^x=k$が異なる3つの実数解をもつ$k$の範囲を求めよ

出典：慶應義塾大学　過去問
この動画を見る　

筑波大　４次関数　接点と交点 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師： 鈴木貫太郎
問題文全文(内容文)：
'93筑波大学過去問題
$f(x)=x^4-2x^2$
f(x)の接線がf(x)と接点以外に異なる2点で交わる条件。
又、接点、2交点の3点が等間隔になるときの接点のx座標
この動画を見る　
PAGE TOP