中１数学「かっこのある方程式」【毎日配信】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中１数学 > 方程式 > 中１数学「かっこのある方程式」【毎日配信】

中１数学「かっこのある方程式」【毎日配信】

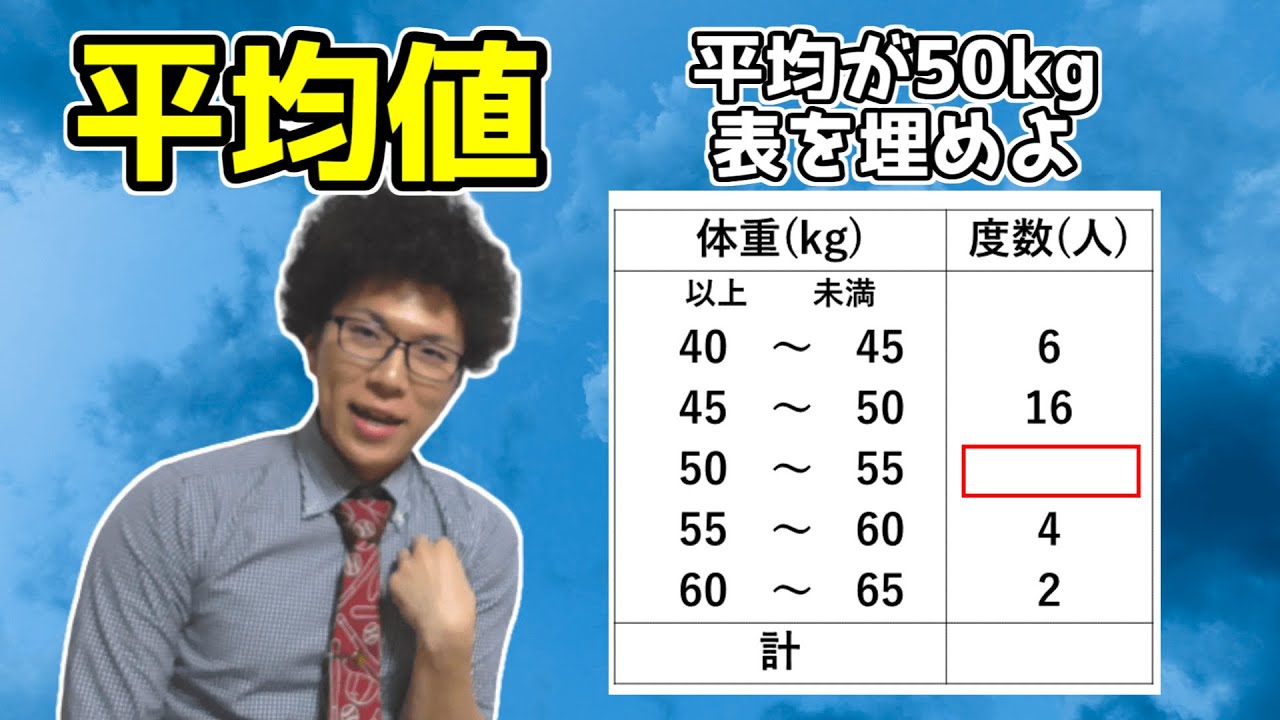
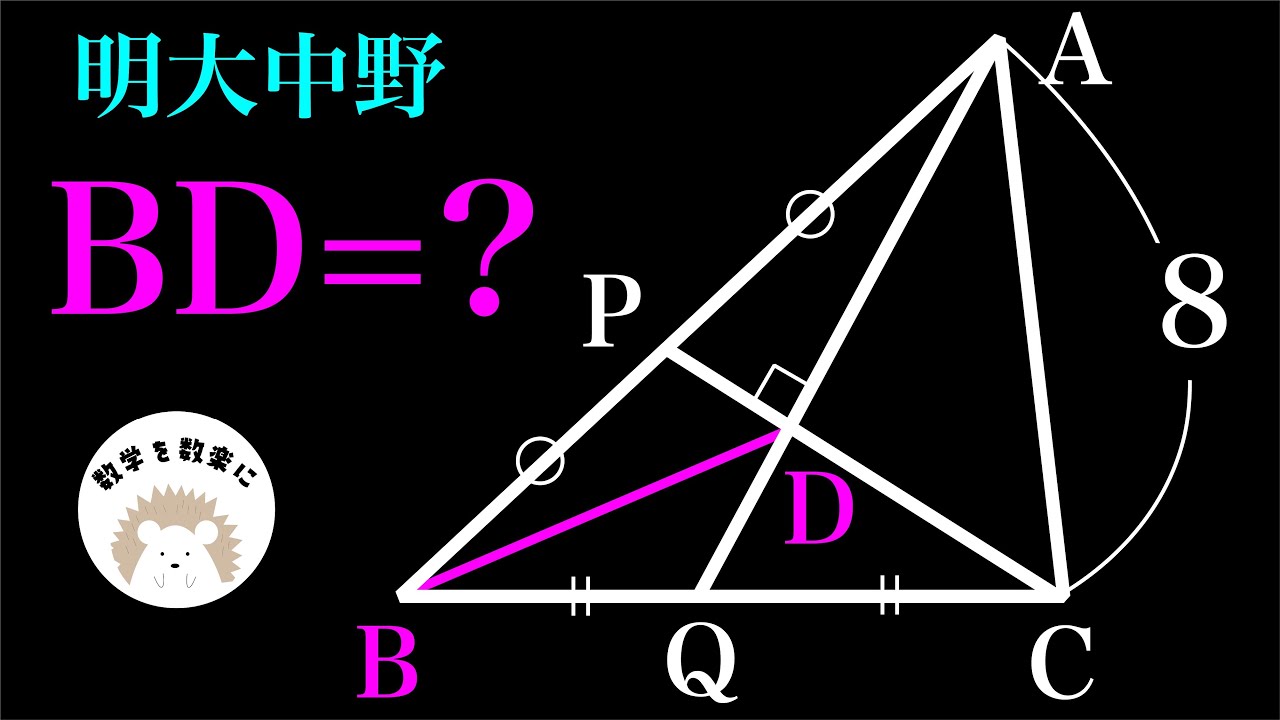
問題文全文(内容文)：
中1~第26回 かっこのある方程式~

例題
次の方程式を解きなさい。

(1)3(x - 4) = 5x + 4　　 (2) 6x - 5(x - 1) = 8

(3) 2(x - 1) = 4(x - 3) 　(4)5-(x-3)=1+(-2x+1)
単元： #数学(中学生)#中１数学#方程式
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第26回 かっこのある方程式~

例題
次の方程式を解きなさい。

(1)3(x - 4) = 5x + 4　　 (2) 6x - 5(x - 1) = 8

(3) 2(x - 1) = 4(x - 3) 　(4)5-(x-3)=1+(-2x+1)
投稿日：2020.10.19

＜関連動画＞

図で理解する球の体積の公式～古森もぐちなぷぷに数学教えてみた～

アイキャッチ画像
単元： #数学(中学生)#中１数学#空間図形
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
球の体積の公式を図を使ってわかりやすく解説します！
この動画を見る　

中学数学苦手対策どうしたらいいですか？

アイキャッチ画像
単元： #数学(中学生)#中１数学#中３数学#方程式#平方根
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
「中学数学苦手対策」について解説しています。
この動画を見る　

図形問題の流れを一発で理解するmovie～全国入試問題解法 #shorts #数学 #math #高校入試

アイキャッチ画像
単元： #数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
図においてxの値を求めなさい.

興南高校過去問
この動画を見る　

【受験対策】　数学－小問①

アイキャッチ画像
単元： #数学(中学生)#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎次の計算をしよう。

①$-5-8 \times \displaystyle \frac{1}{4}$

②$-3+5 \times (-1)^3$

③$4(2x-y)-3(x+y)$

④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$

⑤一次方程式$x-7=9(x+1)$を解こう。

⑥等式$2a-3b=1$を$b$について解こう。

⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
この動画を見る　

【中学数学】正負の数：マイナス×マイナスがなぜプラス？？よくあるこの疑問、私ならこう説明します！！

単元： #数学(中学生)#中１数学#正の数・負の数
指導講師： 理数個別チャンネル
問題文全文(内容文)：
(-60)×(-3)の答えがマイナスになる理由を解説していきます！
この動画を見る　
Back to top