過去一番の良問！重要テクニックだらけの珠玉の一題！【中学受験算数】【入試問題】【成蹊中学校】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 過去一番の良問！重要テクニックだらけの珠玉の一題！【中学受験算数】【入試問題】【成蹊中学校】

過去一番の良問！重要テクニックだらけの珠玉の一題！【中学受験算数】【入試問題】【成蹊中学校】

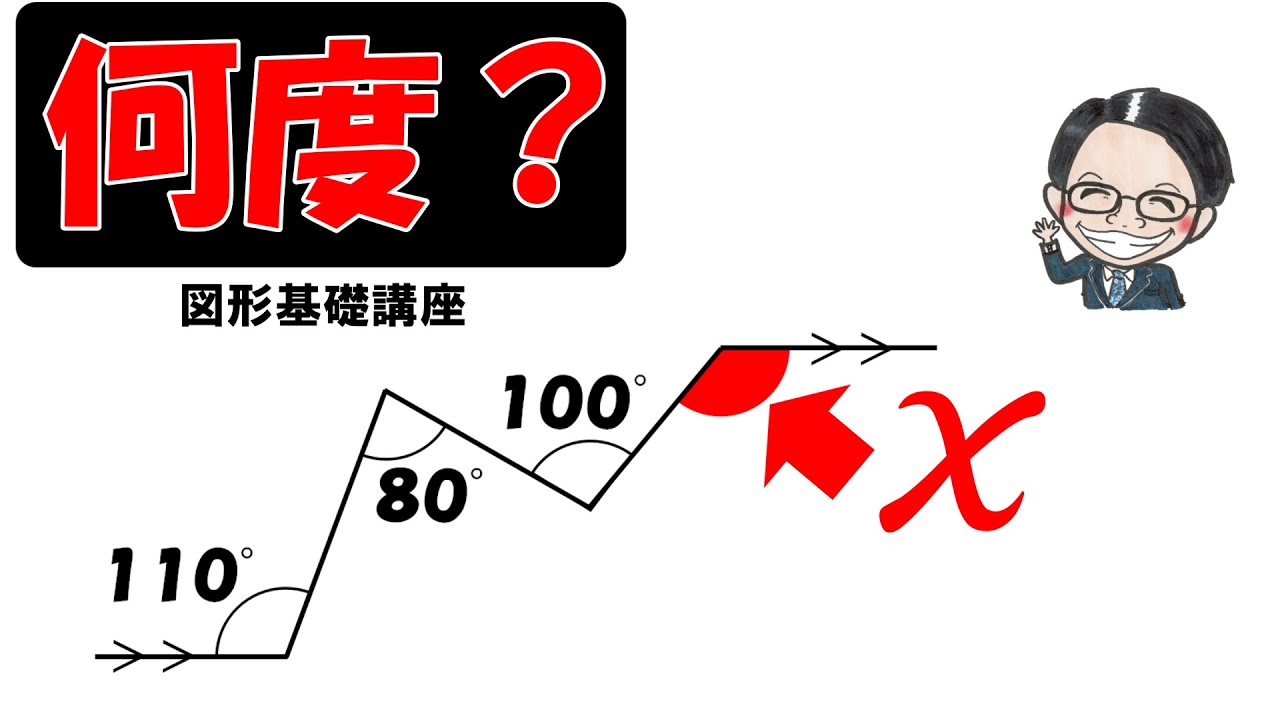
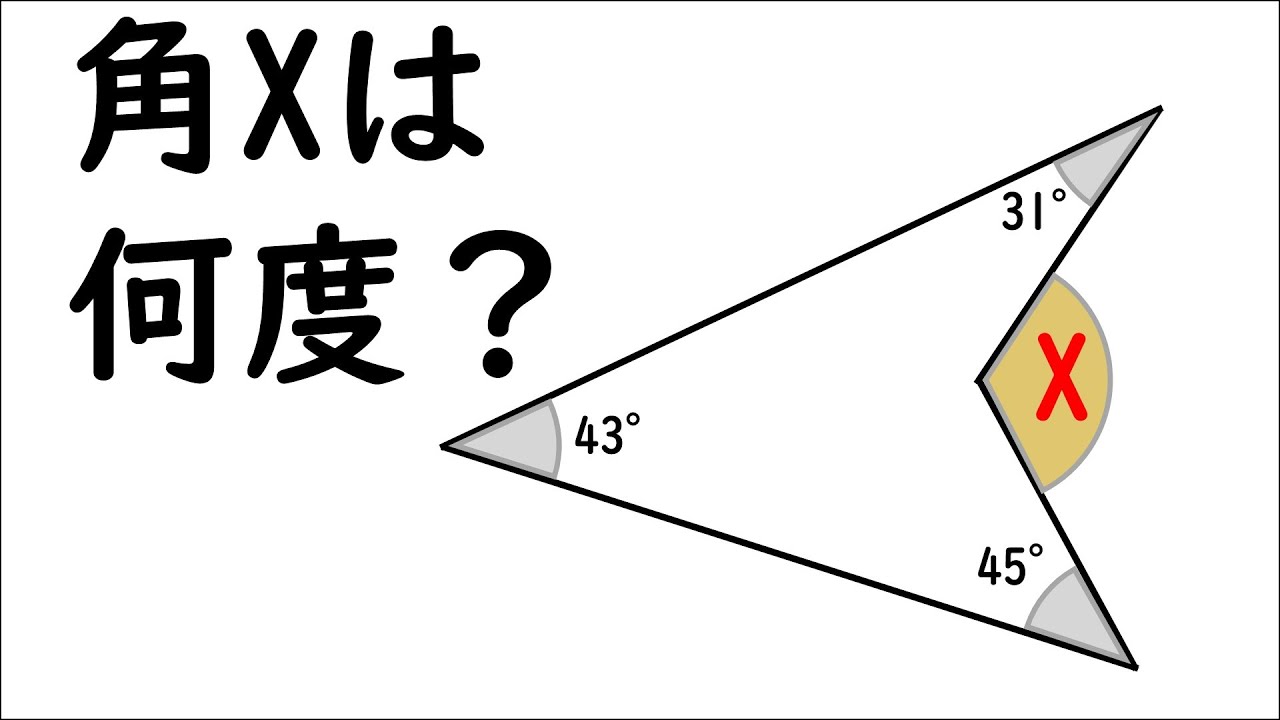
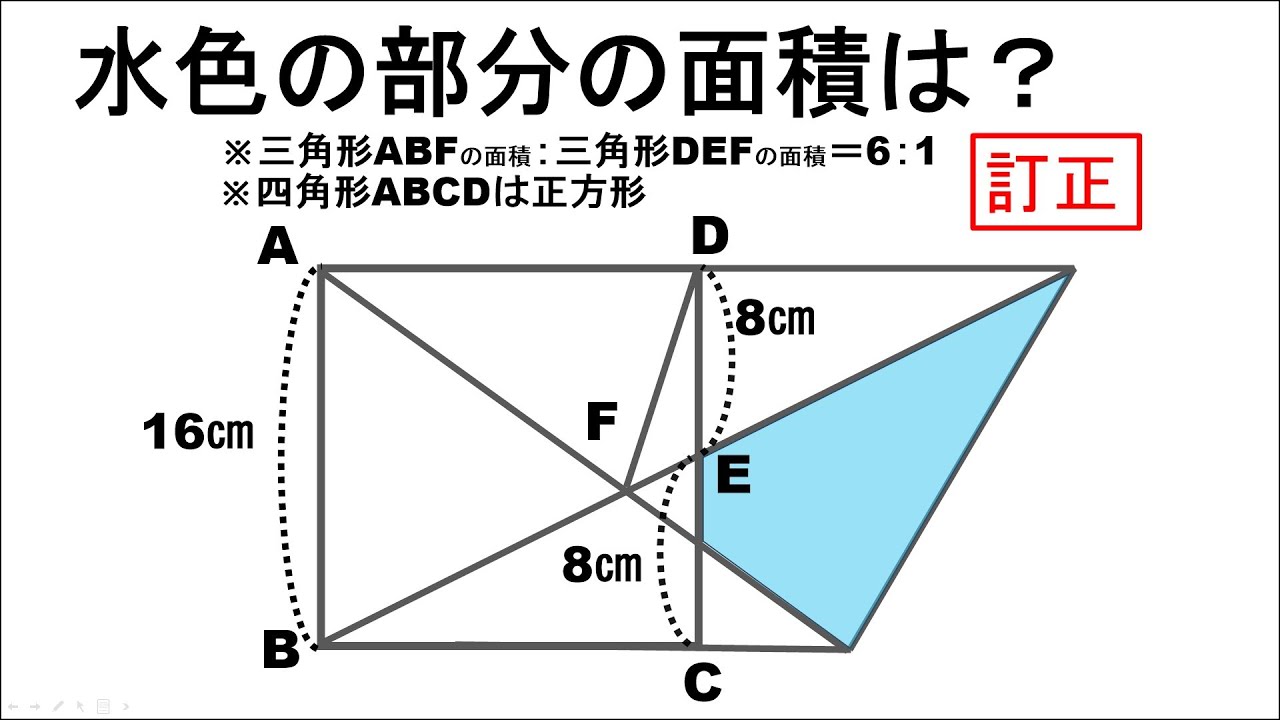
問題文全文(内容文)：
・2021法政大学中学校
下の半円でABは直径、Oは中心です。
このときAE:GCは？

・2011成蹊中学校
左図のように三角形ABCとABを直径とする半円が2点P,Qで交わっている。
APの長さが6㎝のとき(1)～(3)は？
(1)BPの長さ
(2)半円の面積
(3)斜線部の面積

＊図は動画内参照
単元： #算数(中学受験)#平面図形#角度と面積#平面図形その他
指導講師： こばちゃん塾
問題文全文(内容文)：
・2021法政大学中学校
下の半円でABは直径、Oは中心です。
このときAE:GCは？

・2011成蹊中学校
左図のように三角形ABCとABを直径とする半円が2点P,Qで交わっている。
APの長さが6㎝のとき(1)～(3)は？
(1)BPの長さ
(2)半円の面積
(3)斜線部の面積

＊図は動画内参照
投稿日：2022.03.28

＜関連動画＞

小５基礎トレ算数解説１１／１④

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
指導講師： 重吉
問題文全文(内容文)：
【日暦算、カレンダー算】
7/7が日曜日の解き、その年の2/2は何曜日になるか、求めよ。
この動画を見る　

【小５　算数】　　小５－４１　　平行四辺形の面積

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
小５　算数　平行四辺形の面積
以下の問に答えよ
[ポイント] 平行四辺形の面積＝①＿＿＿＿
①＜平行四辺形の図＞　面積（　　　　）㎠
②＜平行四辺形の図＞　面積（　　　　）㎠
③＜平行四辺形の図＞　面積（　　　　）㎠
④＜平行四辺形の図＞　面積（　　　　）㎠
⑤＜方眼上に平行四辺形の図＞　面積（　　　　）㎠
⑥＜平行四辺形の図＞　面積（　　　　）㎠
⑦＜平行四辺形の図＞　面積（　　　　）㎠
※図は動画内参照
この動画を見る　

【受験算数】空間図形：積み木は何個つまれているでしょう【予習シリーズ算数・小5下】

アイキャッチ画像
単元： #算数(中学受験)#立体図形#立体図形その他
教材： #予習シ#予習シ算数・小5下#中学受験教材#立方体・直方体の切断
指導講師： 理数個別チャンネル
問題文全文(内容文)：
下の図は、同じ大きさの立方体の積み木を積み重ねてできた立体を、正面、右側、真上から見た図を表しています。積み重ねてある積み木はなんかでしょう。【予習シリーズ　6年生】【空間図形】
この動画を見る　

【中学受験問題に挑戦】92　（”大人”は頭の体操）正方形を分割（面積問題）

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
問題文
正方形ABCDの面積は？
正方形ABCD 内に2本の直線を引いた。白の面積は５０㎠である。
緑の面積：赤の面積：黄の面積＝３：２：１
※図は動画内参照
この動画を見る　

約数の個数が3個　　専修大学松戸

アイキャッチ画像
単元： #計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
1~50の自然数の中で約数が3コである数は全部で何コ？

専修大学松戸高等学校
この動画を見る　
PAGE TOP