【三平方と√ 禁止】私も超悩みました！最後に驚きの超簡単解法も紹介！【中学受験算数】

問題文全文(内容文)：
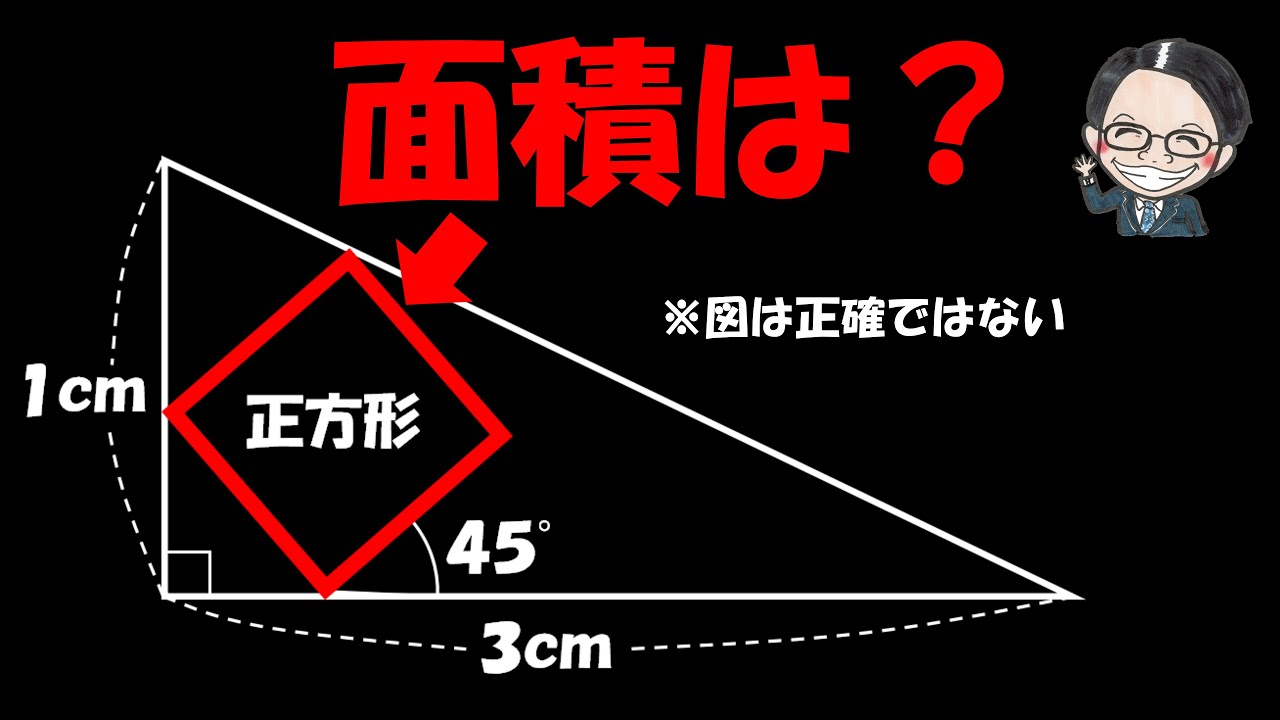
下の四角形ABCDの面積は？
＊図は動画内参照

単元： #算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題

指導講師：こばちゃん塾

問題文全文(内容文)：
下の四角形ABCDの面積は？
＊図は動画内参照

投稿日：2023.10.18

単元： #算数(中学受験)#文章題#仕事算とニュートン算

教材： #予習シ#予習シ算数・小5下#中学受験教材#仕事に関する問題

指導講師：理数個別チャンネル

問題文全文(内容文)：
9人ですると20日かかる仕事があります。この仕事を12人ですると□日で終わります。□にあてはまる数字は？

この動画を見る　

単元： #算数(中学受験)#平面図形#平面図形その他

指導講師：理数個別チャンネル

問題文全文(内容文)：
図のように四角形ABCDのすべての辺をそれぞれ２倍にのばして、四角形EFGHを作りました。四角形EFGHの面積は、四角形ABCDの面積の何倍ですか。

この動画を見る　

単元： #算数(中学受験)#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例

指導講師：数学を数楽に

問題文全文(内容文)：
0.3㎡-120㎠ = ▢㎠

京都学園中学校

この動画を見る　

単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題

指導講師：理数個別チャンネル

問題文全文(内容文)：
A,B2つの整数がある。この2つの整数の積が216、最小公倍数が3888のとき、2つのA,Bの組み合わせをすべて答えよ

この動画を見る　

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#青山学院中等部

指導講師：こばちゃん塾

問題文全文(内容文)：
・左図は2つの合同な正方形が重なったものです。
㋐と㋑の面積比が4：3のとき、㋐と㋑の周の長さの比は？

・左図はたて4㎝、横2㎝の2つの合同な長方形と半径4㎝、中心角60°の4つの合同なおうぎ形を組み合わせたものです。斜線部の面積は？

＊図は動画内参照

この動画を見る　