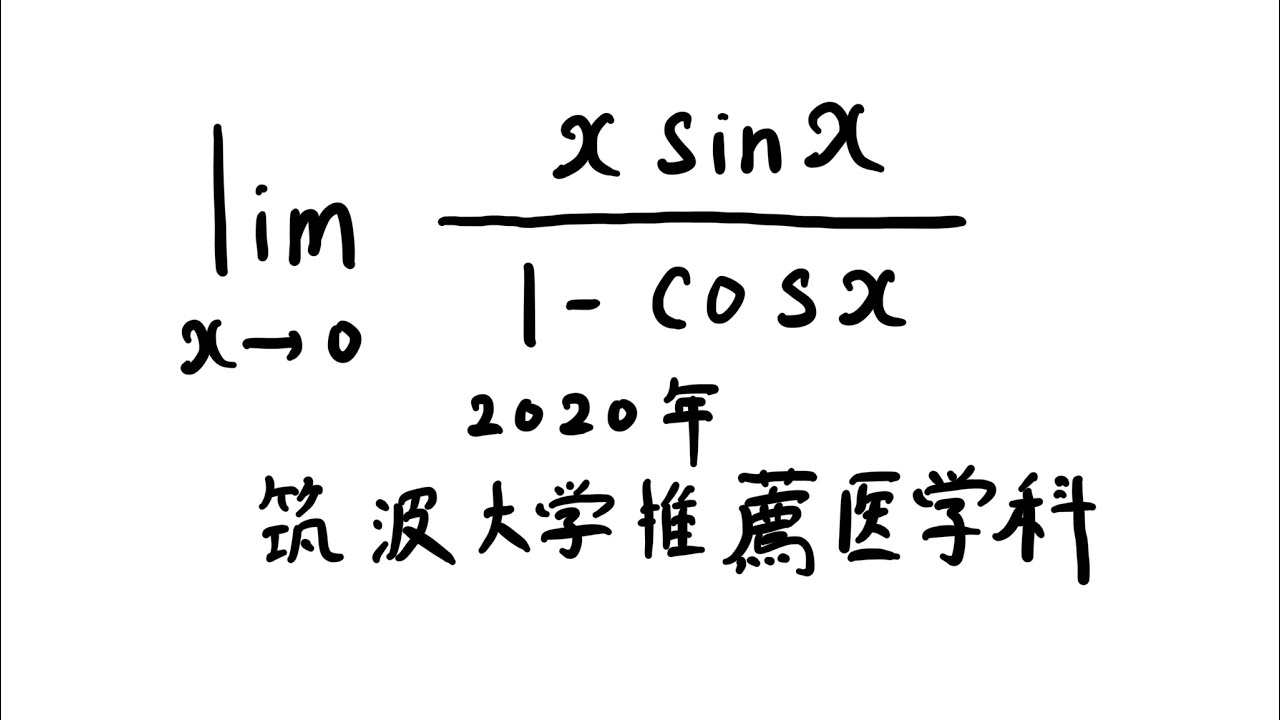【高校数学】無理関数のグラフの裏ワザ！例題もあるよ！

問題文全文(内容文)：
次の無理関数のグラフをかけ。
(1)

y = \sqrt{x + 2}

(2)

y ＝ \sqrt{- 3 x - 6}

(3)

y ＝ - \sqrt{7 - 4 x}

(4)

y ＝ - \sqrt{\frac{1}{2} x - 3}

チャプター：

0:00 問題&無理関数の書き方確認
0:46（１）解説開始！
3:20（２）解説開始！
5:50（３）解説開始！
8:11（４）解説開始！

単元： #関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の無理関数のグラフをかけ。
(1)

y = \sqrt{x + 2}

(2)

y ＝ \sqrt{- 3 x - 6}

(3)

y ＝ - \sqrt{7 - 4 x}

(4)

y ＝ - \sqrt{\frac{1}{2} x - 3}

投稿日：2024.02.12

＜関連動画＞

数学「大学入試良問集」【17−3② 解けない漸化式とはさみうちの原理】を宇宙一わかりやすく

単元： #大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：

a_{1} = 2, a_{n + 1} = \frac{4 a_{n}^{2} + 9}{8 a_{n}} (n = 1, 2, 3, ・ ・ ・)

で定義される数列

{a_{n}}

について以下の問いに答えよ。
（1）

a_{n} > \frac{3}{2} (n = 1, 2, 3, ・ ・ ・)

を証明せよ。
（2）

a_{n + 1} - \frac{3}{2} < \frac{1}{3} {[a_{n} - \frac{3}{2}]}^{2} (n = 1, 2, 3, ・ ・ ・)

を証明せよ。
（3）

lim_{n \to \infty} a_{n}

を求めよ。

この動画を見る　

【0≦θ≦πを問題文に追加】微分すると大変かも・・・　By ～らん～

単元： #数Ⅱ#三角関数#三角関数とグラフ#数列#数列とその和（等差・等比・階差・Σ）#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数列の極限#関数の極限#数学(高校生)#数B#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：

m, n

：自然数

m ≧ 2

f (θ) = \frac{\sin n θ}{\cos n θ + m}

の最大値を

α (m, n)

とする

\sum_{m = 2}^{\infty} {α (m, n)}^{2}

を求めよ

この動画を見る　

【概要欄に正確な文章と説明の補足】大学入試問題#76　京都大学(2007)　数列と極限

単元： #大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：

x, y

：異なる正の実数

a_{1} = 0

a_{n + 1} = x a_{n} = s a_{n} + y^{n + 1}

のとき

lim_{n \to \infty} a_{n} < \infty

となるような

(x, y)

の範囲を図示せよ。

出典：2007年京都大学　入試問題

この動画を見る　

数検準1級1次過去問（7番　極限値）

単元： #数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：

lim_{n \to \infty} n {l o g (n + 3) - l o g n}

lim_{n \to \infty} (1 + \frac{1}{n})^{n} = lim_{n \to 0} (1 + n)^{\frac{1}{n}} = e

この動画を見る　

11奈良県教員採用試験（数学：高校3番逆関数と積分）

単元： #数Ⅱ#指数関数と対数関数#指数関数#対数関数#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#面積・体積・長さ・速度#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：

高　

f (x) = \frac{e^{x} + e^{- x}}{2}

(x ≧ 0)

の逆関数をg(x)
(1)g(x)を求めよ。
(2)y=g(x),x=2,x軸で囲まれた面積

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【高校数学】無理関数のグラフの裏ワザ！例題もあるよ！

＜関連動画＞

数学「大学入試良問集」【17−3② 解けない漸化式とはさみうちの原理】を宇宙一わかりやすく

【0≦θ≦πを問題文に追加】微分すると大変かも・・・ By ～らん～

【概要欄に正確な文章と説明の補足】大学入試問題#76 京都大学(2007) 数列と極限

数検準1級1次過去問（7番 極限値）

11奈良県教員採用試験（数学：高校3番 逆関数と積分）