問題文全文(内容文):
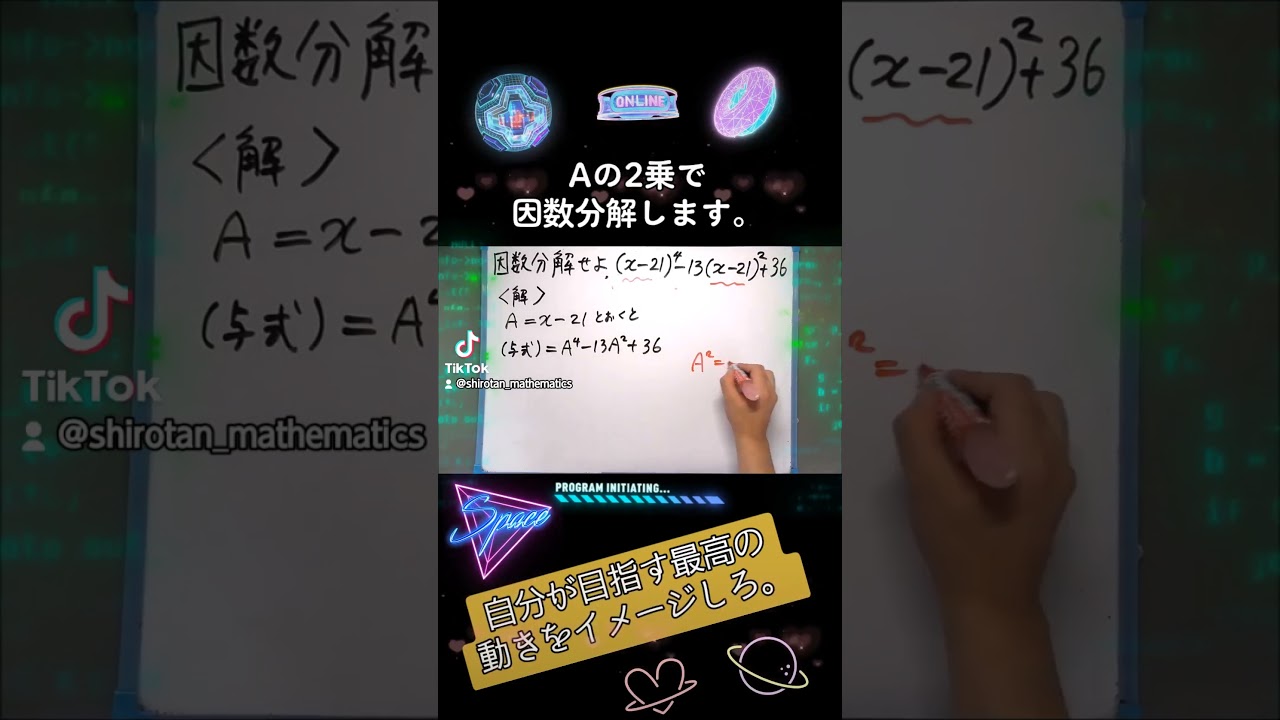
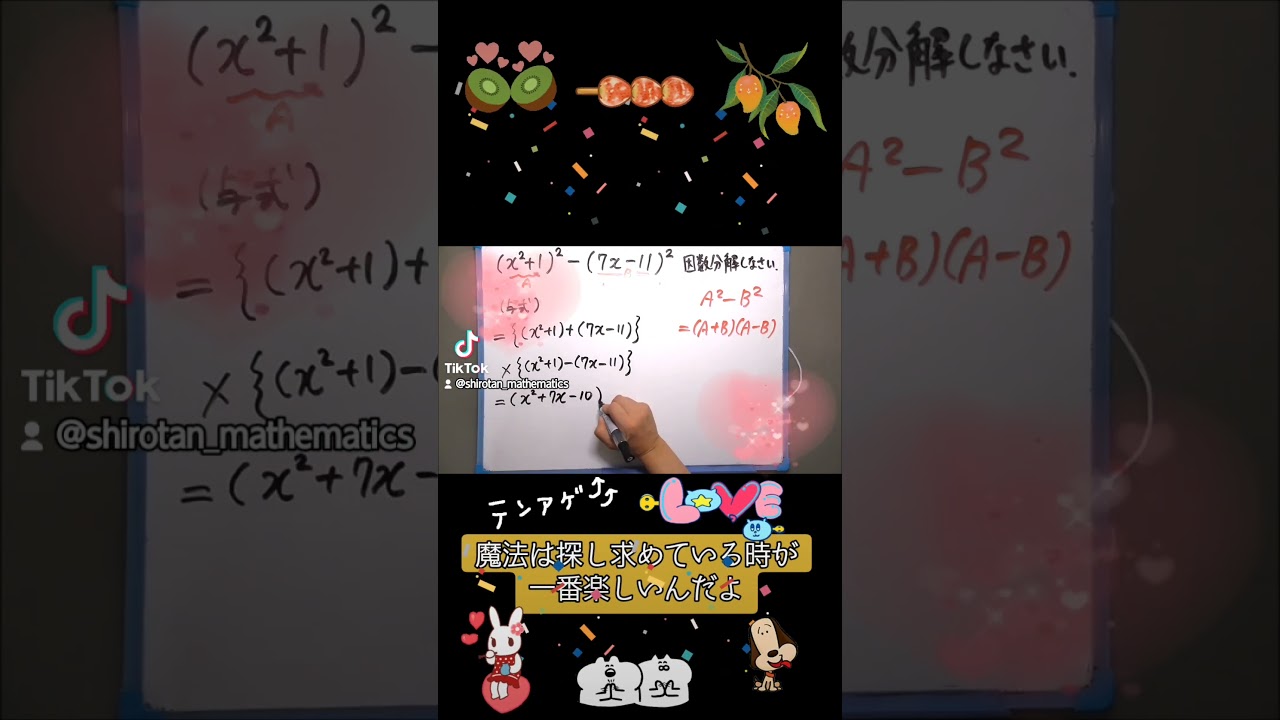
$\frac{x+2y}{xy} = \frac{1}{4}$のとき$\frac{6}{x}+\frac{3}{y} =?$
芝浦工業大学柏高等学校
$\frac{x+2y}{xy} = \frac{1}{4}$のとき$\frac{6}{x}+\frac{3}{y} =?$
芝浦工業大学柏高等学校
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x+2y}{xy} = \frac{1}{4}$のとき$\frac{6}{x}+\frac{3}{y} =?$
芝浦工業大学柏高等学校
$\frac{x+2y}{xy} = \frac{1}{4}$のとき$\frac{6}{x}+\frac{3}{y} =?$
芝浦工業大学柏高等学校
投稿日:2021.10.15