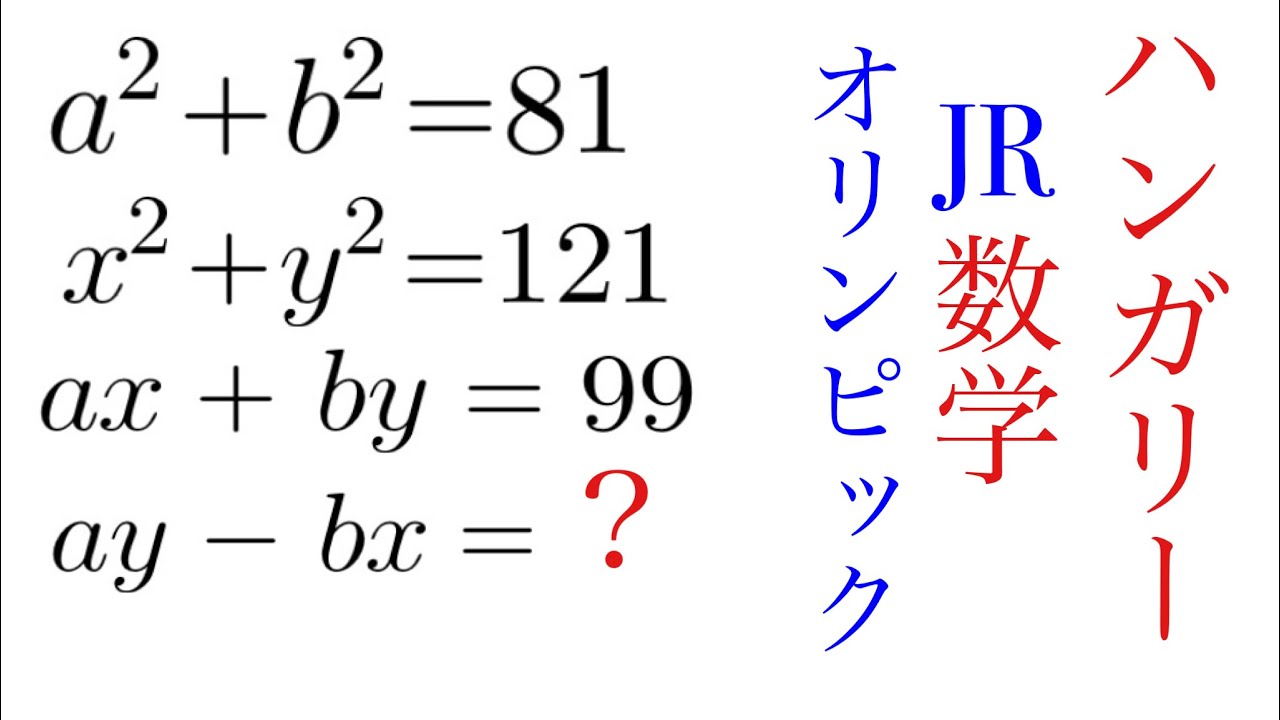福田のおもしろ数学050〜数学オリンピックの問題〜2変数関数の最小

問題文全文(内容文)：
実数a,bが$a+b=17$を満たすとき$2^a+4^b$の最小値を求めよ

数学オリンピック過去問

単元： #数学検定・数学甲子園・数学オリンピック等#数学オリンピック

指導講師：福田次郎

問題文全文(内容文)：
実数a,bが$a+b=17$を満たすとき$2^a+4^b$の最小値を求めよ

数学オリンピック過去問

投稿日：2024.02.13

＜関連動画＞

福田のおもしろ数学140〜不等式の証明とRavi変換

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#恒等式・等式・不等式の証明#数学オリンピック#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$a$, $b$, $c$が三角形の3辺の長さのとき次の不等式を証明せよ。
$a^2(b+c-a)$+$b^2(c+a-b)$+$c^2(a+b-c)$≦$3abc$

この動画を見る　

Japanese Mathematics Olympic Question 2016 数学オリンピック

単元： #数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#場合の数#数学オリンピック#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
How many possible ways are there to divide this 11×11 grid into 5 rectangles.
where one of them must not share any of its side with the original rectangle(11×11).
Do not consider any rotation or flipping.

この動画を見る　

数学オリンピック本戦　整数問題

単元： #数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
数学オリンピック
$2^a+3^b+1=6^c$
a,b,c自然数
すべて求めよ。

この動画を見る　

数学オリンピック日本予選　合同式の基本

単元： #数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$1111^{2018}$を$11111$で割ったあまりを求めよ.

数学オリンピック過去問

この動画を見る　

練習問題35　数学オリンピックの問題　複素数を利用して証明してみた。

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学オリンピック#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 福田のおもしろ数学050〜数学オリンピックの問題〜2変数関数の最小

＜関連動画＞

福田のおもしろ数学140〜不等式の証明とRavi変換

Japanese Mathematics Olympic Question 2016 数学オリンピック

数学オリンピック本戦 整数問題

数学オリンピック日本予選 合同式の基本

練習問題35 数学オリンピックの問題 複素数を利用して証明してみた。