福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 立体図形 > 立体切断 > 福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面

福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面

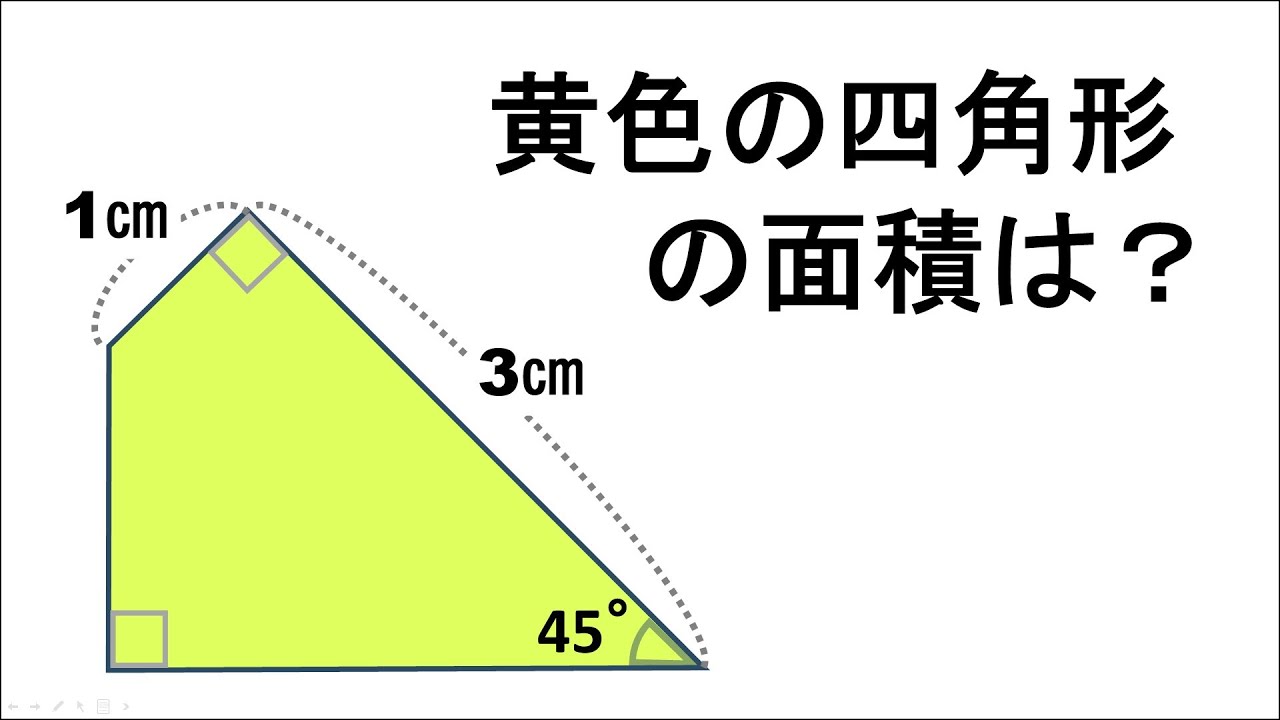
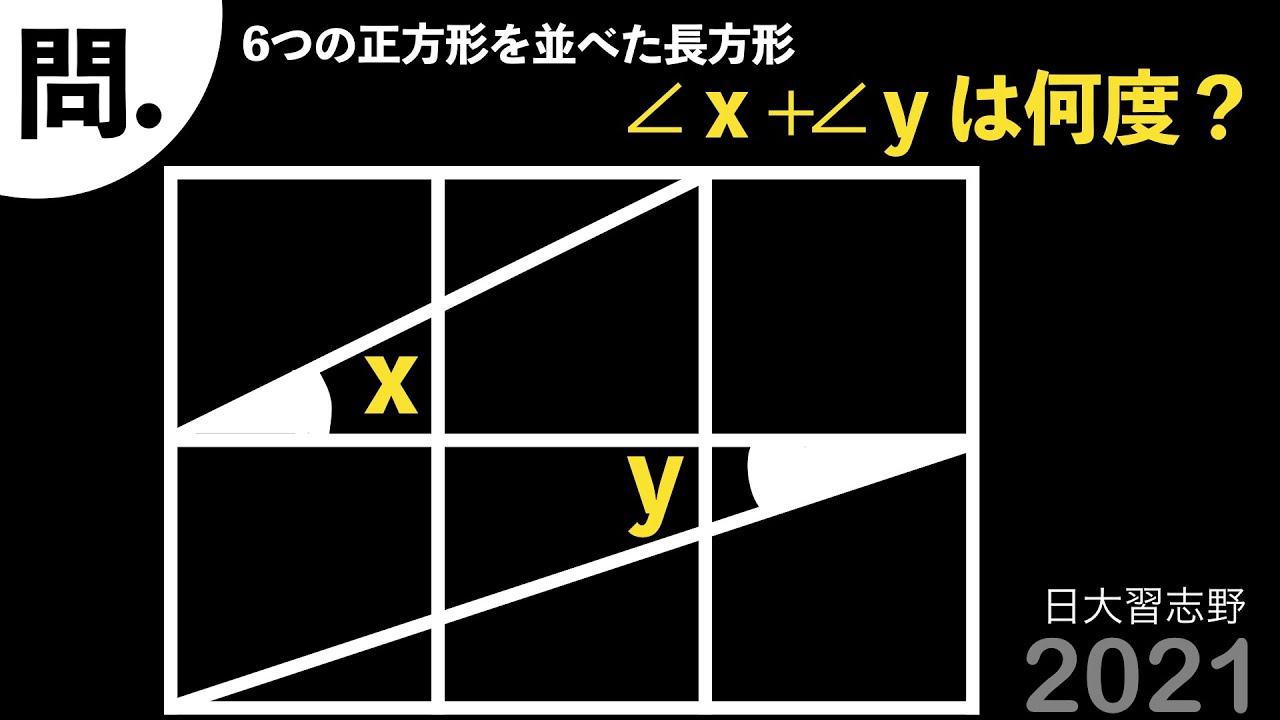
問題文全文(内容文)：
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①～⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
単元： #算数(中学受験)#立体図形#立体切断
指導講師： 福田次郎
問題文全文(内容文)：
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①～⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
投稿日：2024.05.08

＜関連動画＞

【受験算数】規則性：〇番目の数の求め方　ややこしい群数列も考えていこう！

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
指導講師： 理数個別チャンネル
問題文全文(内容文)：
100 99 98 97 96 99 98 97 96 95 98 97 96 95 …
上記のように並んでいる数列がある。
(1)127番目の数はいくつですか？
(2)51が3回目に出てくるのは何番目ですか？
この動画を見る　

【中学受験問題に挑戦】17　（”大人”は頭の体操）　 おうぎ形と正方形の面積比

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
黄色の面積:青の面積=?:?
を求めよ。
※円周率は3.14
この動画を見る　

【受験算数】仕事算（練習❹）給水管と排水管【予習シリーズ算数・小5下】

アイキャッチ画像
単元： #算数(中学受験)#文章題#仕事算とニュートン算
教材： #予習シ#予習シ算数・小5下#中学受験教材#仕事に関する問題
指導講師： 理数個別チャンネル
問題文全文(内容文)：
2本の給水管A,Bと、排水管Cがついた水そうがあります。Cを開いたままで、Aを使って給水すると12分間、Bを使って給水すると36分間で水そうがいっぱいになります。また、いっぱいになった水をA,Bを閉じて、Cで排水すると9分間で水そうは空になります。これについて、次の問いに答えなさい。
(1)A,Bの1分間の給水量の比を求めなさい。
(2)Cを閉じて、A,Bの両方を使って水を入れると、水そうがいっぱいになるまでに何分かかりますか。
この動画を見る　

実は超簡単！？重要なセオリーがたくさん詰まった良問！【中学受験算数】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
下図のxは何度？
この動画を見る　

【算数練習】70　（”大人”は頭の体操）

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
青線(辺DN)の長さを求めよ。

・直線MNは台形ABCD
の面積を2等分している。

・AMの長さ=BMの長さ

※図は動画内参照
この動画を見る　
PAGE TOP