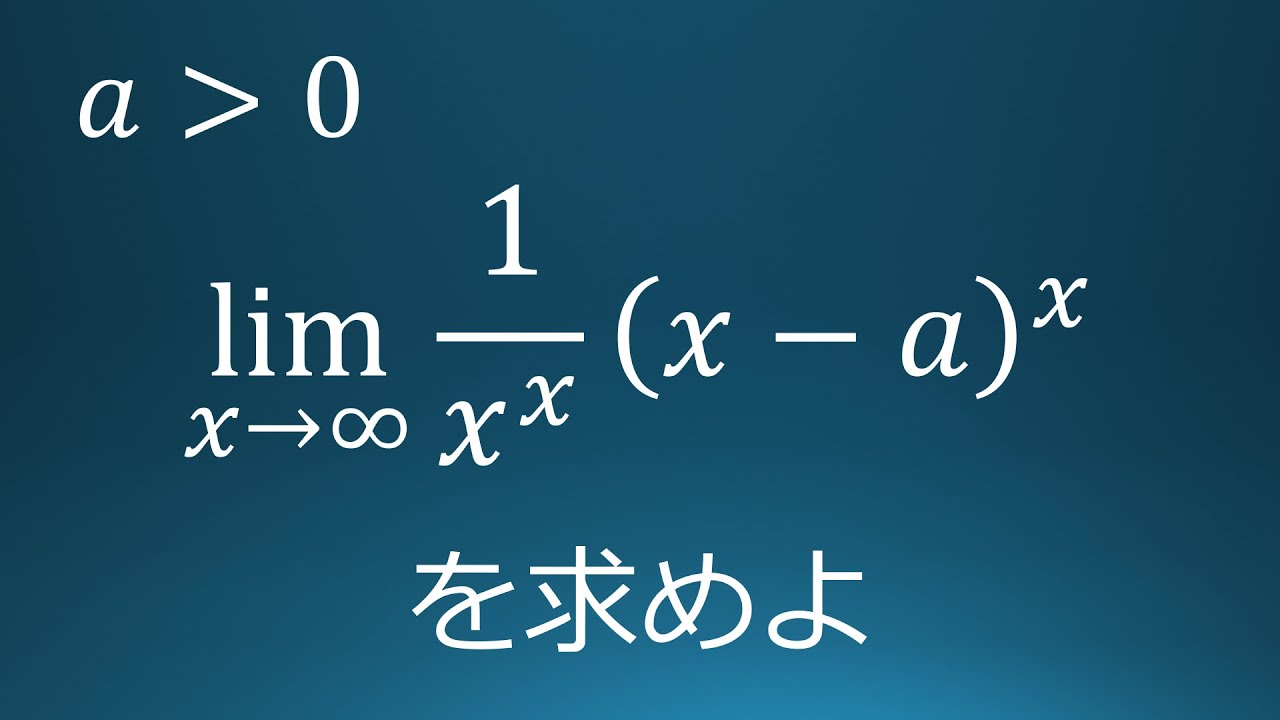【数Ⅲ】極限：極限の定形不定形をマスターしよう！ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅲ > 関数と極限 > 数列の極限 > 【数Ⅲ】極限：極限の定形不定形をマスターしよう！

【数Ⅲ】極限：極限の定形不定形をマスターしよう！

問題文全文(内容文)：
極限の考え方の基本です。変形が必要な場合と必要でない場合の違いをチェックしましょう！
チャプター：

0:00 OP
0:30 極限の定形、不定形とは
5:05 実践
8:10 ED

単元： #関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師： 理数個別チャンネル
問題文全文(内容文)：
極限の考え方の基本です。変形が必要な場合と必要でない場合の違いをチェックしましょう！
投稿日：2021.12.09

＜関連動画＞

大学入試問題#453「落とせない問題」　信州大学(2022)　#定積分

アイキャッチ画像
単元： #大学入試過去問(数学)#対数関数#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{dx}{x(1+log\ x^3)log\ x}$

出典：2022年信州大学　入試問題
この動画を見る　

ハルハルさん作成問題　#極限の存在範囲

アイキャッチ画像
単元： #関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{\sqrt{ (1+\displaystyle \frac{a^2}{x})(1+\displaystyle \frac{a}{x})(1+\displaystyle \frac{b}{x}) }-1}{x^b}=\displaystyle \frac{b^2}{a}+1$
を満たす実数の組$(a,b)$を平面上に図示せよ
この動画を見る　

福田のわかった数学〜高校３年生理系089〜グラフを描こう(11)分数関数、凹凸、漸近線

アイキャッチ画像
単元： #関数と極限#微分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師： 福田次郎
問題文全文(内容文)：
数学$\textrm{III}$　グラフを描こう(11)

$y=\frac{x^3}{x^2-1}$　のグラフを描け。ただし、凹凸、漸近線も調べよ。
この動画を見る　

福田のわかった数学〜高校３年生理系025〜極限(25)関数の極限、三角関数の極限(5)

アイキャッチ画像
単元： #関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師： 福田次郎
問題文全文(内容文)：
数学$\textrm{III}$　三角関数の極限(5)
$\lim_{x \to 0}\displaystyle \frac{\tan x°}{x}$　を求めよ。
この動画を見る　

分母が奇数の分数を無限に足したい引いたり、何故か答えにπが登場

アイキャッチ画像
単元： #関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots=\dfrac{\pi}{4}$
この動画を見る　
PAGE TOP