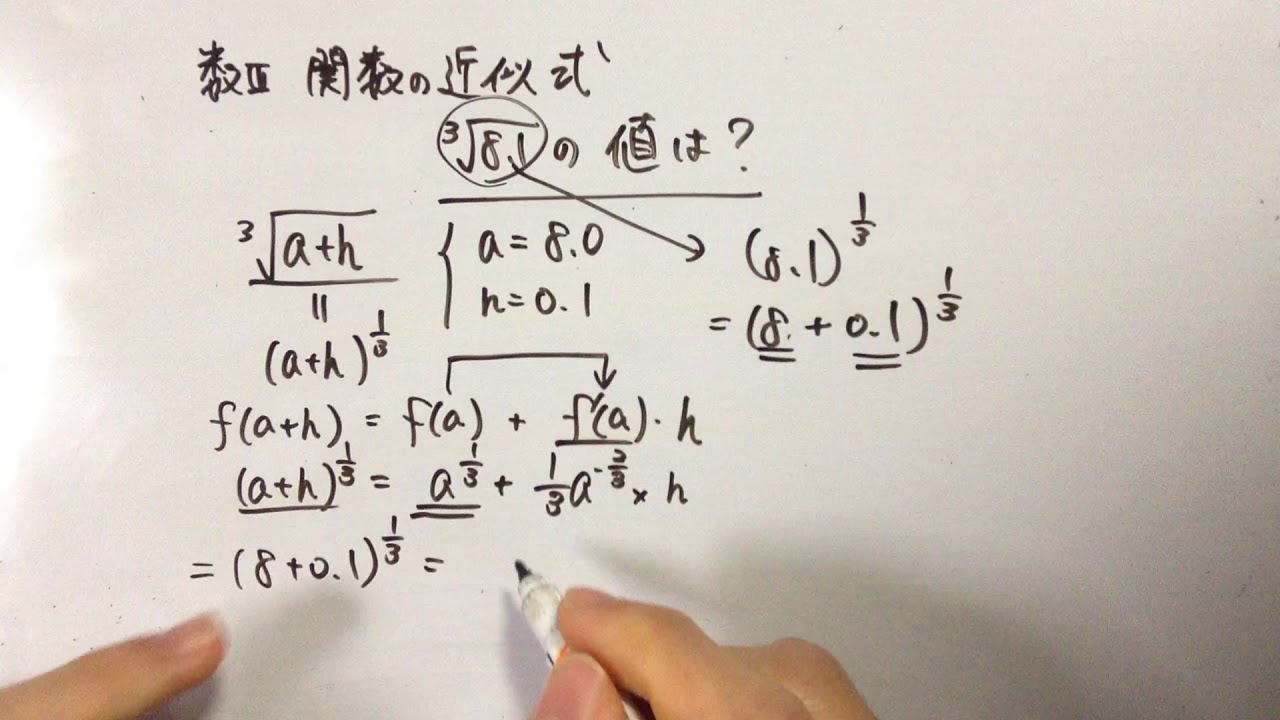問題文全文(内容文):
$e^x$の$x=0$における4次近似式を用いて
$\sqrt{e}$
の近似値を小数第4位まで求めよ.
$e^x$の$x=0$における4次近似式を用いて
$\sqrt{e}$
の近似値を小数第4位まで求めよ.
単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$e^x$の$x=0$における4次近似式を用いて
$\sqrt{e}$
の近似値を小数第4位まで求めよ.
$e^x$の$x=0$における4次近似式を用いて
$\sqrt{e}$
の近似値を小数第4位まで求めよ.
投稿日:2021.07.12