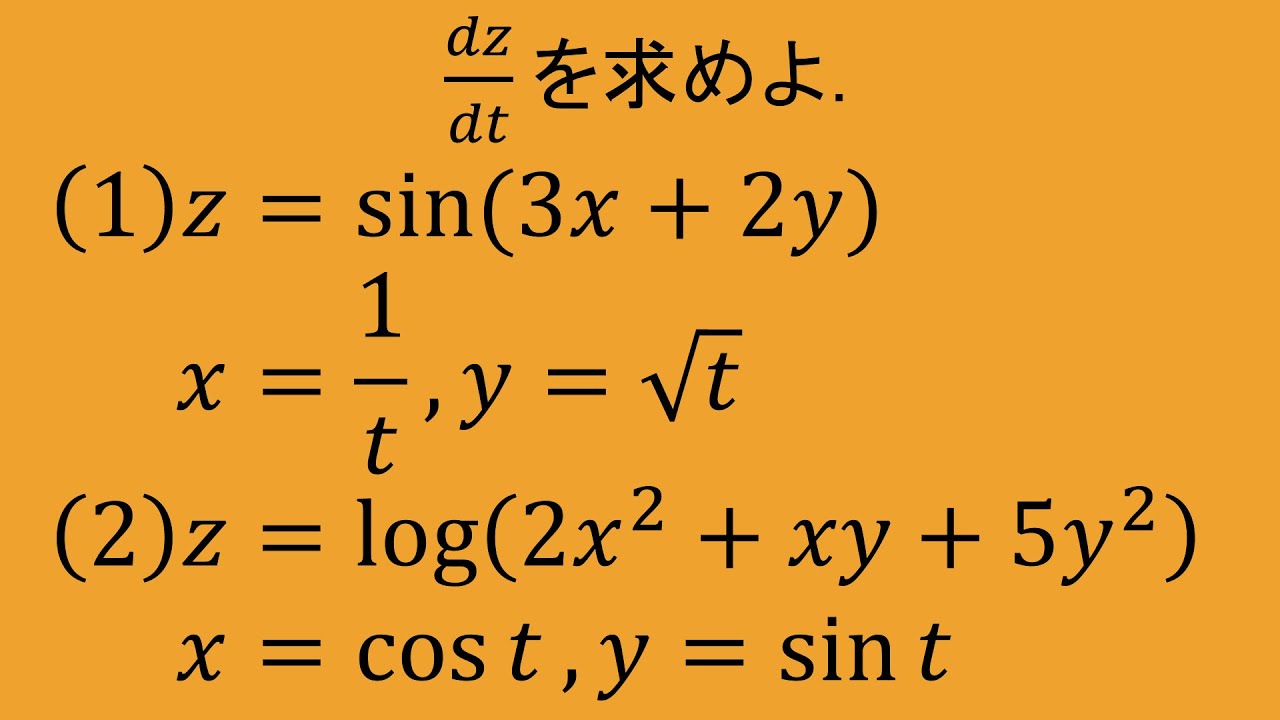高専数学微積I #259(2) 広義積分

問題文全文(内容文)：
$\displaystyle \int_{e}^{\infty}\dfrac{1}{r(\log r)^2} dr$
を計算せよ.

単元： #数Ⅱ#微分法と積分法#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{e}^{\infty}\dfrac{1}{r(\log r)^2} dr$
を計算せよ.

投稿日：2021.07.03

単元： #計算と数の性質#数の性質その他#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$30^{2020}$の下2021ケタ目の数は？

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$n$は自然数である.
$x^{6n}$を$x^4+x^2+1$で割った余りを求めよ.

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
05年　山口大学

次の方程式 $x^3-kx+2=0$において$k$ が実数であるときの実数解の個数を求めよ。

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$(3x^3-4x^2+10x+4)^2$を$x^2-2x+4$で割ったあまりを求めよ.$

この動画を見る　

単元： #数Ⅱ#図形と方程式#円と方程式#数学(高校生)

教材： #高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
$x^2+y^2+4x-6y+13=0$はどのような図形を表しているか？

この動画を見る　