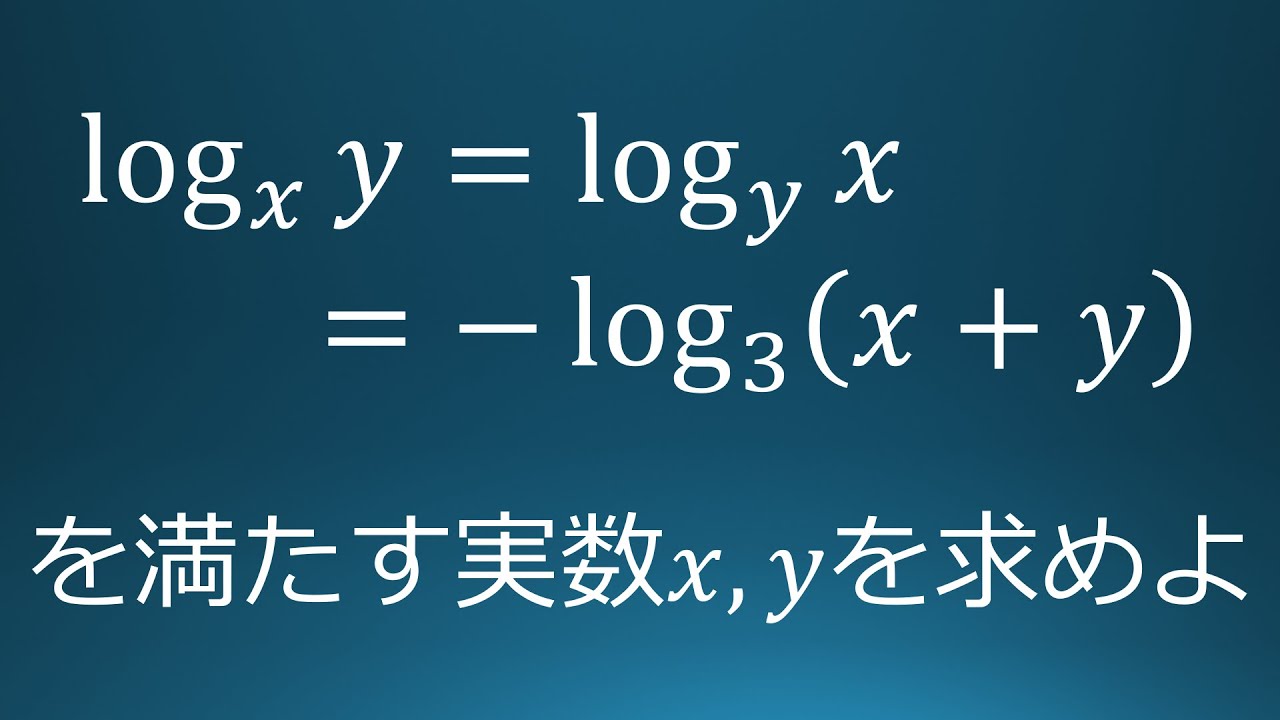問題文全文(内容文):
$x,y$は実数であり,$x\gt 0,y\gt 0$である.
$xy^{1+\log_2 x^2}=1$を満たすとき,$xy$のとりうる値の範囲を求めよ.
2021東京女子医大過去問
$x,y$は実数であり,$x\gt 0,y\gt 0$である.
$xy^{1+\log_2 x^2}=1$を満たすとき,$xy$のとりうる値の範囲を求めよ.
2021東京女子医大過去問
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は実数であり,$x\gt 0,y\gt 0$である.
$xy^{1+\log_2 x^2}=1$を満たすとき,$xy$のとりうる値の範囲を求めよ.
2021東京女子医大過去問
$x,y$は実数であり,$x\gt 0,y\gt 0$である.
$xy^{1+\log_2 x^2}=1$を満たすとき,$xy$のとりうる値の範囲を求めよ.
2021東京女子医大過去問
投稿日:2021.01.31