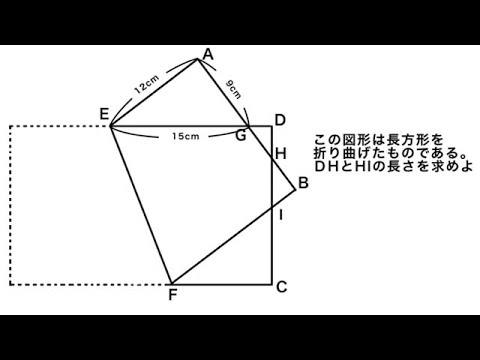
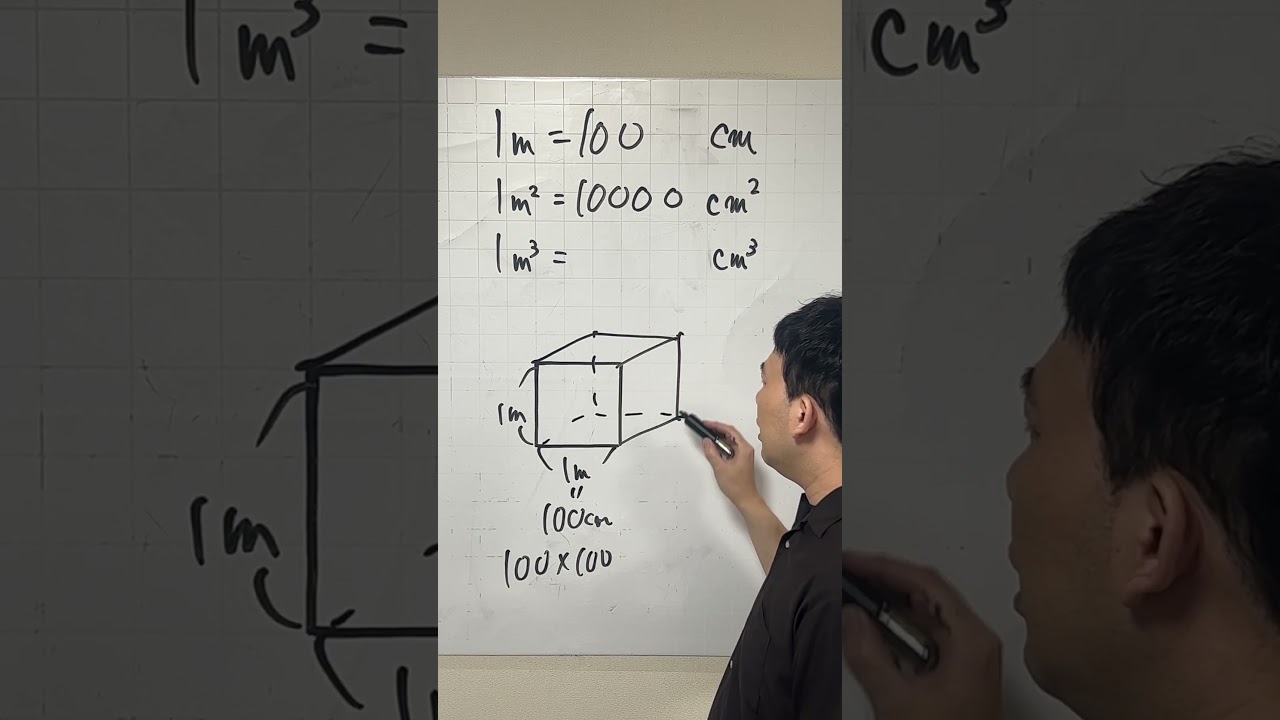
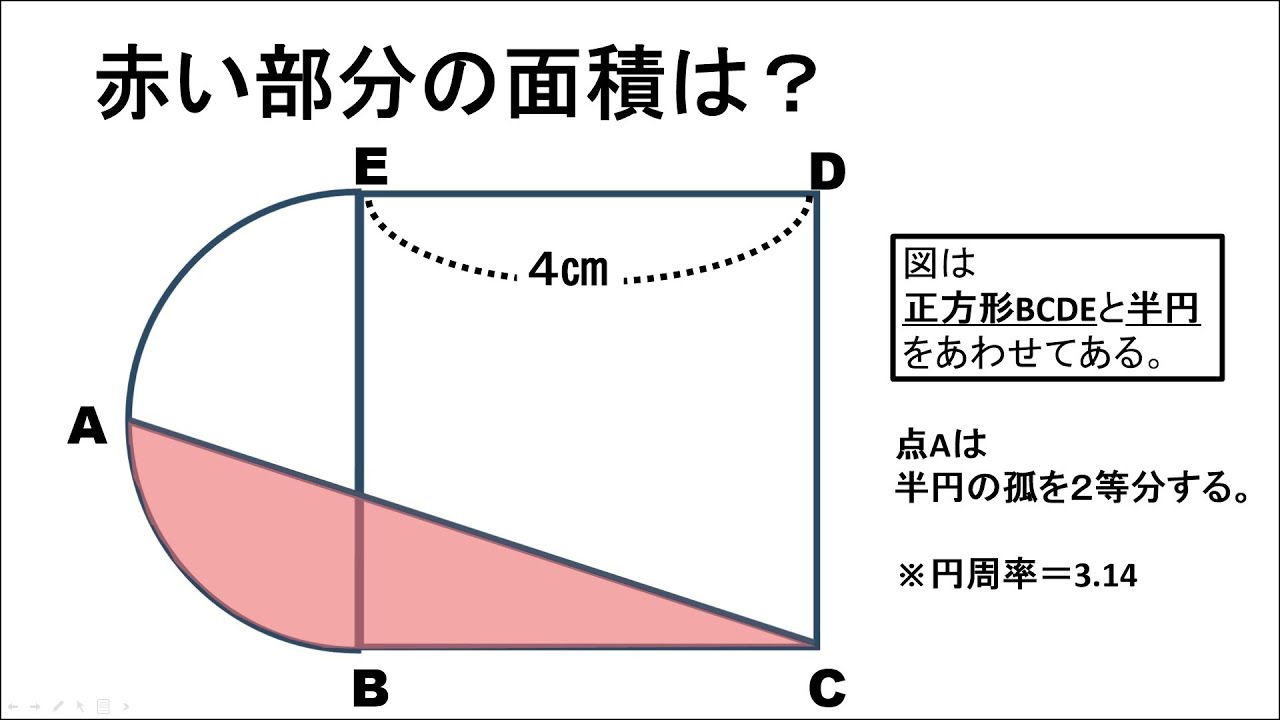
問題文全文(内容文):
中空方陣(基本)
おはじきを外側の一辺の数が10個、はば3列の中空方陣に並べたいと思います。おはじきは何個いりますか。
中空方陣(応用)
1.赤色のおはじきを使って、5列の中空方陣を作りました。次に、青色のおはじきを使って、この方陣の中空部をうめましたが、まだ青色のおはじきが51個残っていたので、方陣の外側のまわりを1列で囲もうとしたら、33個不足しました。赤色と青色とではどちらが何個多いですか。
中空方陣(基本)
おはじきを外側の一辺の数が10個、はば3列の中空方陣に並べたいと思います。おはじきは何個いりますか。
中空方陣(応用)
1.赤色のおはじきを使って、5列の中空方陣を作りました。次に、青色のおはじきを使って、この方陣の中空部をうめましたが、まだ青色のおはじきが51個残っていたので、方陣の外側のまわりを1列で囲もうとしたら、33個不足しました。赤色と青色とではどちらが何個多いですか。
チャプター:
0:00 オープニング
0:02 1)基本
2:08 2)応用
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
中空方陣(基本)
おはじきを外側の一辺の数が10個、はば3列の中空方陣に並べたいと思います。おはじきは何個いりますか。
中空方陣(応用)
1.赤色のおはじきを使って、5列の中空方陣を作りました。次に、青色のおはじきを使って、この方陣の中空部をうめましたが、まだ青色のおはじきが51個残っていたので、方陣の外側のまわりを1列で囲もうとしたら、33個不足しました。赤色と青色とではどちらが何個多いですか。
中空方陣(基本)
おはじきを外側の一辺の数が10個、はば3列の中空方陣に並べたいと思います。おはじきは何個いりますか。
中空方陣(応用)
1.赤色のおはじきを使って、5列の中空方陣を作りました。次に、青色のおはじきを使って、この方陣の中空部をうめましたが、まだ青色のおはじきが51個残っていたので、方陣の外側のまわりを1列で囲もうとしたら、33個不足しました。赤色と青色とではどちらが何個多いですか。
投稿日:2024.08.06