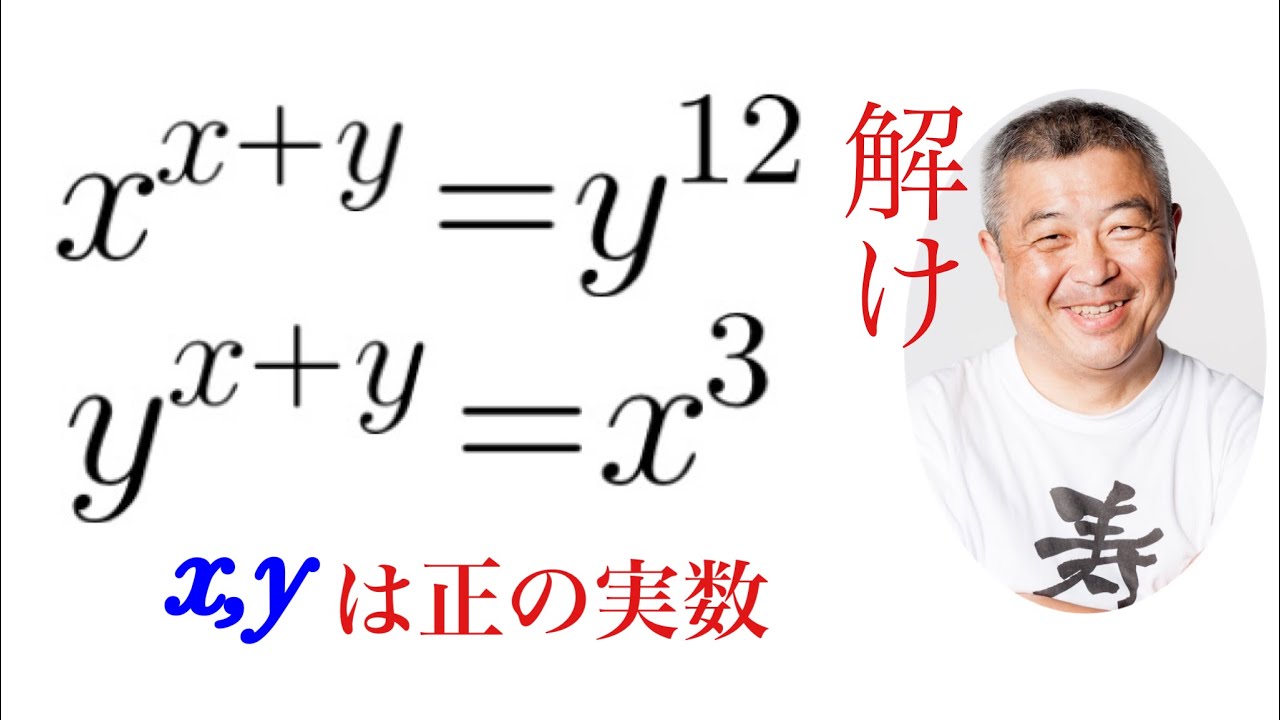問題は解けるようにできている。指数の計算早実

問題文全文(内容文)：
$\frac{(-3)^{20}-(-3)^{15} \times 81}{4} -3^{19}$

早稲田実業学校

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{(-3)^{20}-(-3)^{15} \times 81}{4} -3^{19}$

早稲田実業学校

投稿日：2023.01.06

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
紙を42回折ったときの紙の厚さなど　解説動画です

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\dfrac{4x^2}{1+4x^2}=y$
$\dfrac{4y^2}{1+4y^2}=z$
$\dfrac{4z^2}{1+4z^2}=x$
これを解け.

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$2^{55},3^{44},4^{33},5^{22}$を小さい順に並べなさい。

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#その他#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
6⃣$4^x+9^y=a^2$
$2^{x+1}+3^{2y}$の最大値を求めよ。（a>1）

この動画を見る　

単元： #数Ⅱ#式と証明#指数関数と対数関数#整式の除法・分数式・二項定理#指数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$1.11^{111}$と$1111$どっちが大きい？？

この動画を見る　