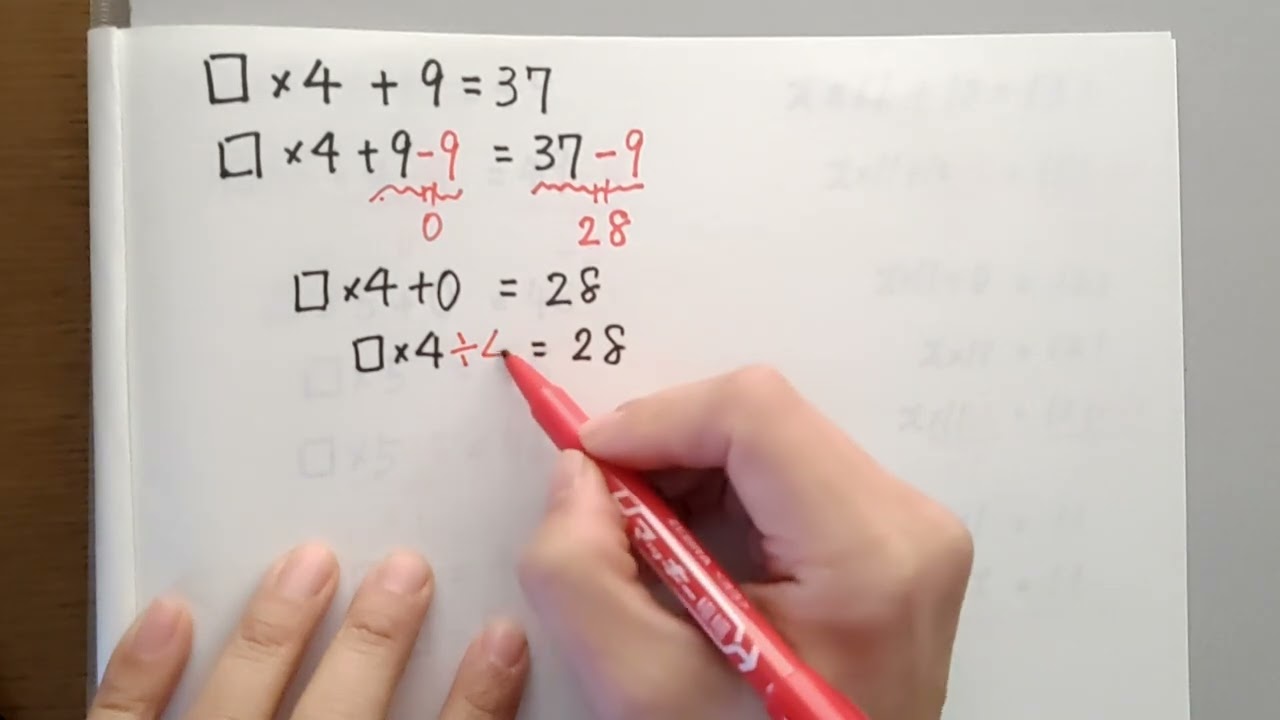問題文全文(内容文)：
自然数$n$に対して
$\sqrt{n}$に最も近い奇数を$a_n$とする。
最も近い奇数が$2$つあるときはその小さい方とする。
$a_{2025}$を求めて下さい。
自然数$n$に対して
$\sqrt{n}$に最も近い奇数を$a_n$とする。
最も近い奇数が$2$つあるときはその小さい方とする。
$a_{2025}$を求めて下さい。
単元：
#計算と数の性質#数の性質その他#数学(高校生)
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
自然数$n$に対して
$\sqrt{n}$に最も近い奇数を$a_n$とする。
最も近い奇数が$2$つあるときはその小さい方とする。
$a_{2025}$を求めて下さい。
自然数$n$に対して
$\sqrt{n}$に最も近い奇数を$a_n$とする。
最も近い奇数が$2$つあるときはその小さい方とする。
$a_{2025}$を求めて下さい。
投稿日：2025.03.30
