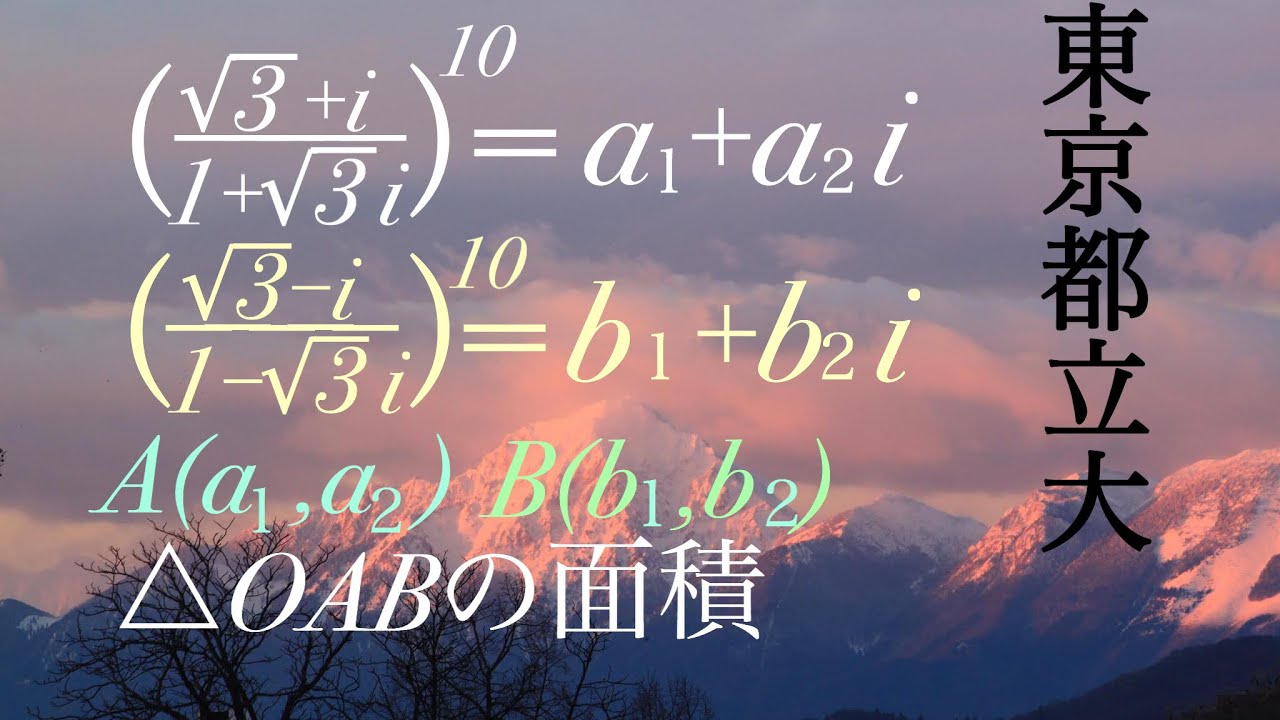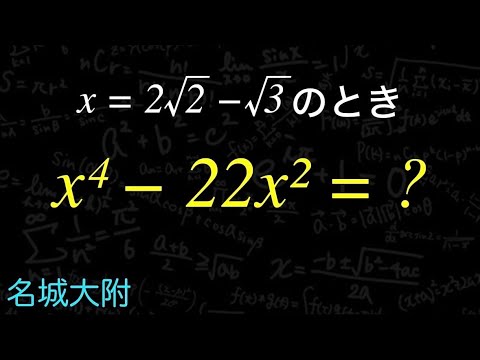問題文全文(内容文):
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典:2021年一橋大学後期 入試問題
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典:2021年一橋大学後期 入試問題
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典:2021年一橋大学後期 入試問題
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典:2021年一橋大学後期 入試問題
投稿日:2024.02.05