【受験算数】三角形の中にある三角形②【予習シリーズ算数・小5下】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 【受験算数】三角形の中にある三角形②【予習シリーズ算数・小5下】

【受験算数】三角形の中にある三角形②【予習シリーズ算数・小5下】

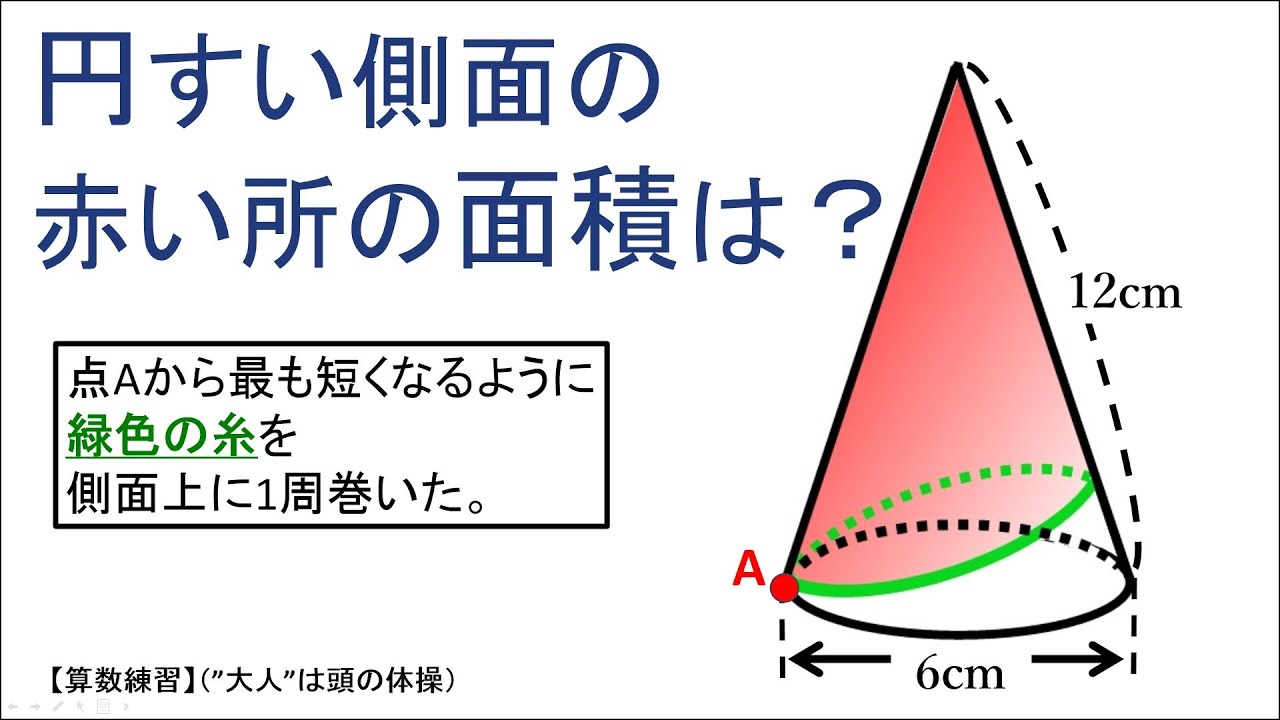
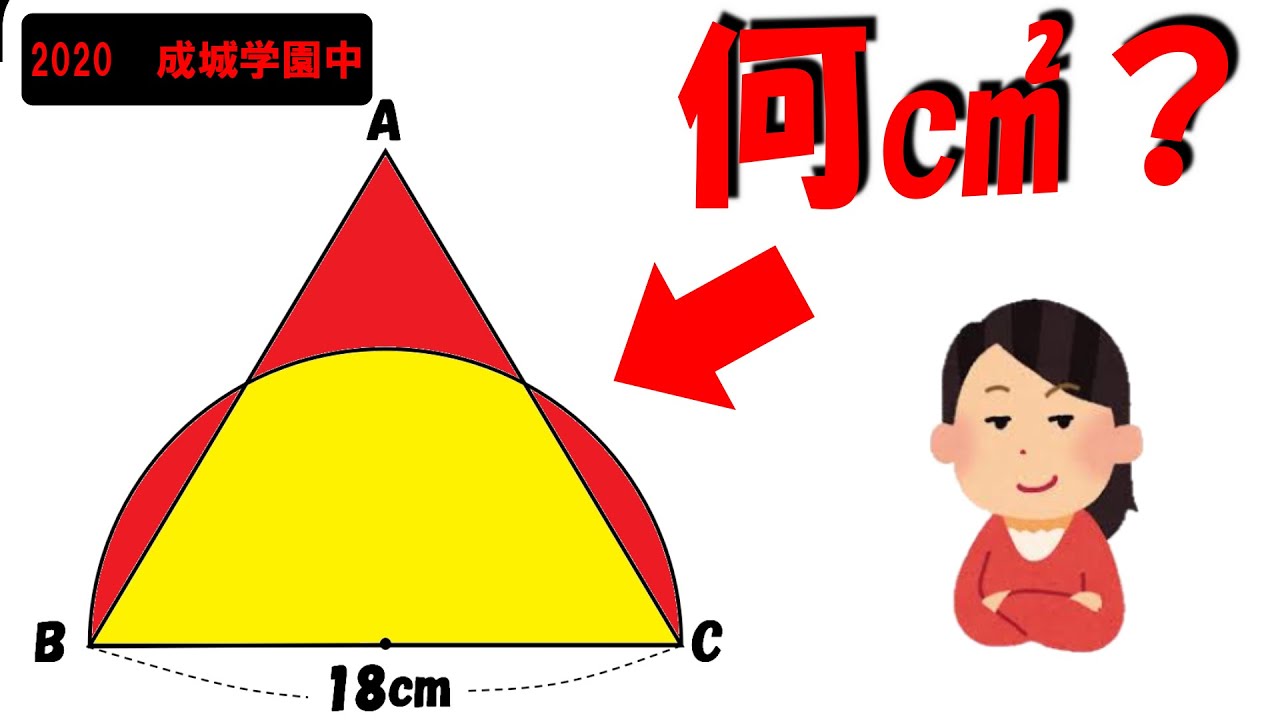
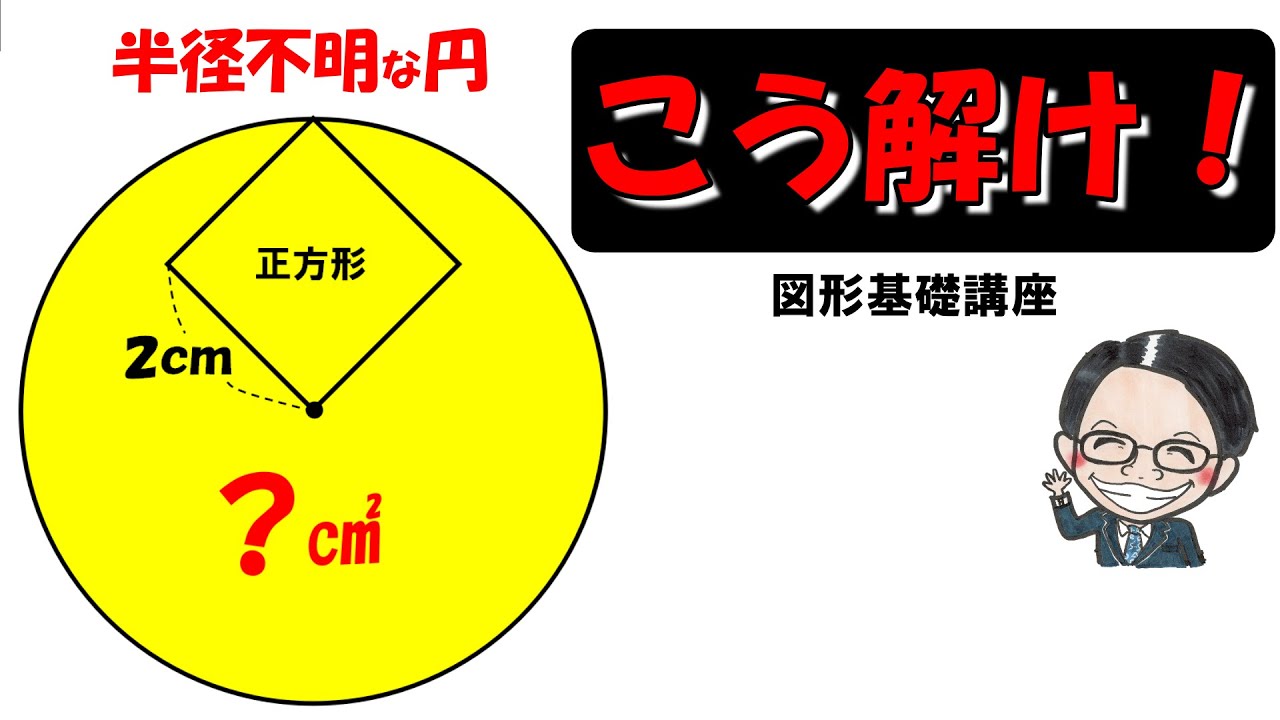
問題文全文(内容文)：
右の図の点D,E,Fは、三角形ABCの各辺をそれぞれ延長した直線上にあり、
AB:BD＝2:3
BC:CE＝1:2
CA:AF＝1:3
です。このとき、次の比を求めなさい。
(1)三角形ABCと三角形BDEの面積の比
(2)三角形ABCと三角形DEFの面積の比
チャプター：

0:11 問題の捉え方
0:32 補助線の引き方

単元： #算数(中学受験)#平面図形#角度と面積
教材： #予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師： 理数個別チャンネル
問題文全文(内容文)：
右の図の点D,E,Fは、三角形ABCの各辺をそれぞれ延長した直線上にあり、
AB:BD＝2:3
BC:CE＝1:2
CA:AF＝1:3
です。このとき、次の比を求めなさい。
(1)三角形ABCと三角形BDEの面積の比
(2)三角形ABCと三角形DEFの面積の比
投稿日：2023.01.19

＜関連動画＞

【算数練習】27　（”大人”は頭の体操）

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
台形の面積問題、台形の面積と三角形の面積の理解を問う問題を解説します。
この動画を見る　

【受験算数】規則性：１から順番に2の倍数と3の倍数以外の数を並べていくと、「299」は何番目の数になるか？

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
指導講師： 理数個別チャンネル
問題文全文(内容文)：
１から順番に2の倍数と3の倍数以外の数を並べていくと、「299」は何番目の数になるか？
この動画を見る　

【受験算数】拡大・縮小：台形DFGEと台形FBCGの面積比を求めなさい。

アイキャッチ画像
単元： #算数(中学受験)#平面図形#相似と相似を利用した問題
教材： #SPX#6年算数W-支援#中学受験教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
右の図形で、DE、FG、BCは平行です。
（1）DEの長さは何cmですか。
（2）三角形ABCと三角形ADEの面積比を求めなさい。
（3）台形DFGEと台形FBCGの面積比を求めなさい。
この動画を見る　

中学受験算数「割合①」（百分率・歩合）小学４年生～６年生対象【毎日配信】

アイキャッチ画像
単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第15回割合①

例1
小数で表した割合は百分率で、百分率で表した割合は 小数で表しなさい。
(1)0.03= (2)0.276= (3)40.3%= (4)150%=

小数で表した割合は歩合で、歩合で表した割合は 小数で表しなさい。
(1) 0.375=
(2) 0.068 =
(3)7割 =
(4) 3割9厘=
この動画を見る　

【視聴者様リクエスト動画】円錐の中心角と側面積を一瞬で求める超便利公式！どうして成り立つかも説明します！

アイキャッチ画像
単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師： こばちゃん塾
問題文全文(内容文)：
円錐の中心角と側面積を求める公式解説
この動画を見る　
PAGE TOP