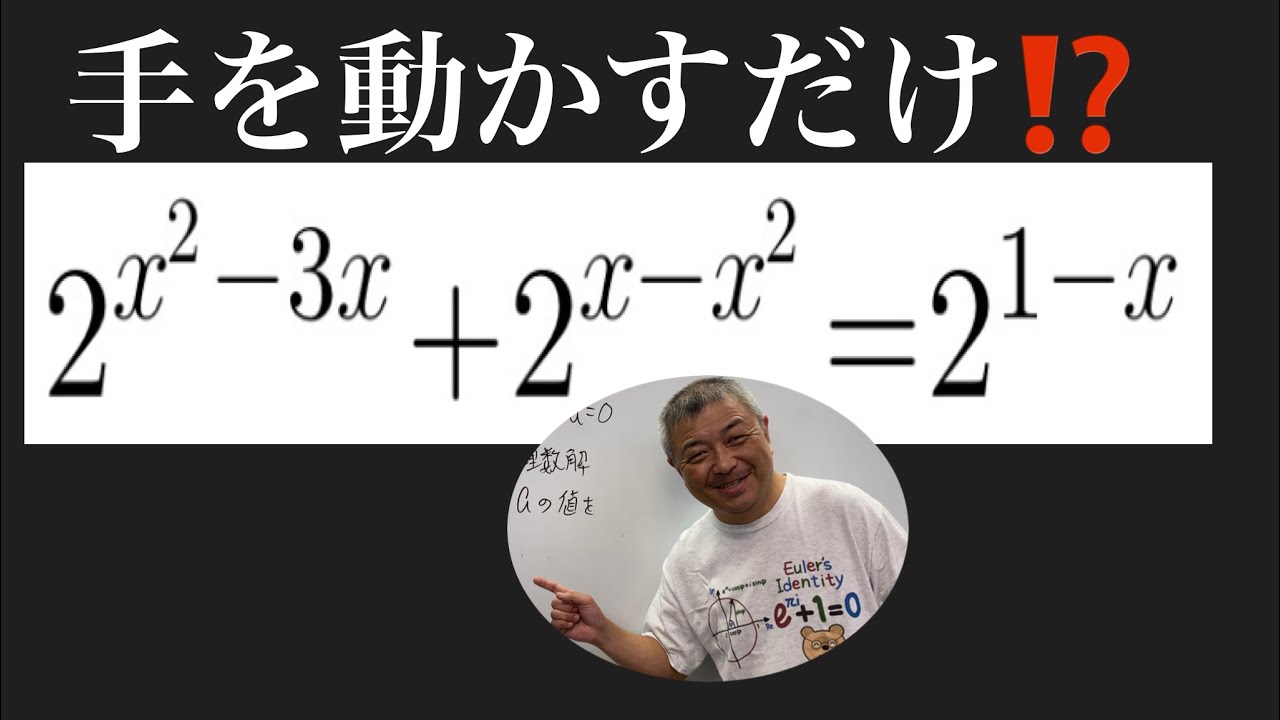問題文全文(内容文):
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
チャプター:
0:00 オープニング
0:04 導入 この問題、何がゴール?
1:21 座標の表し方について
2:14 2点を通る直線の傾きとは?
4:23 エンディング
単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
投稿日:2025.02.19