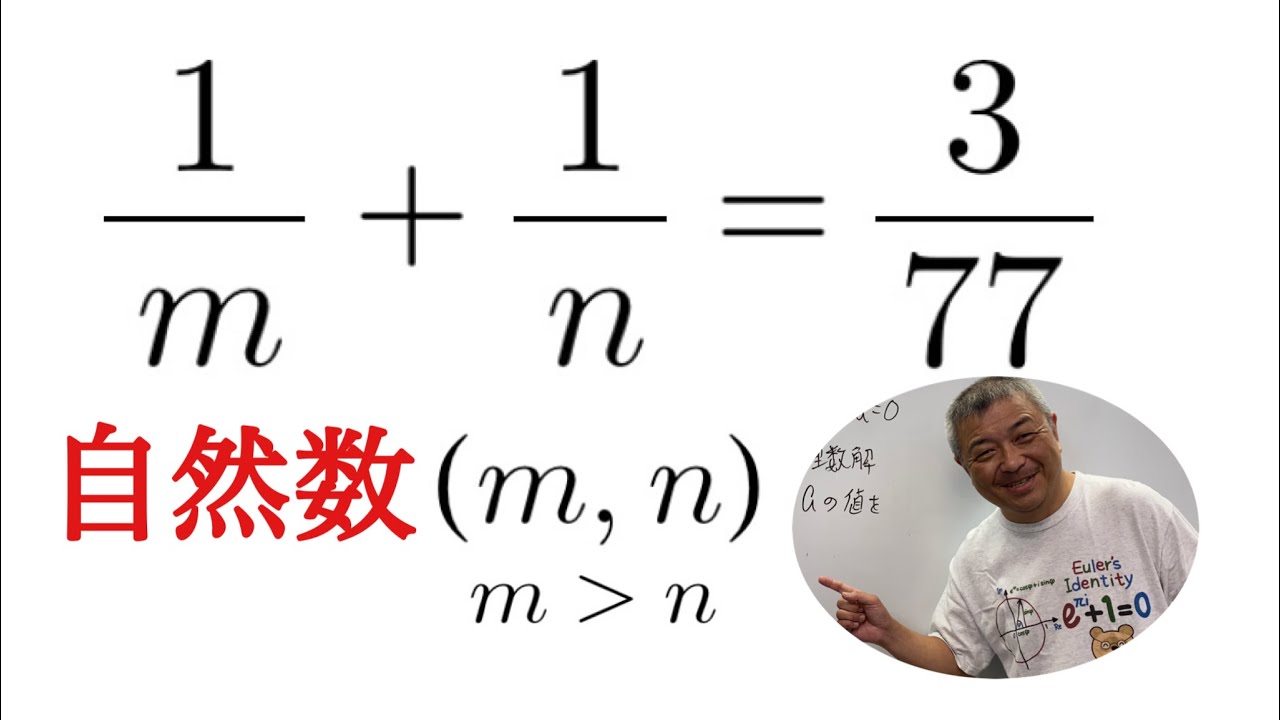問題文全文(内容文):
$3^a-2^n=1$ $a,b \varepsilon Z$
(1)
$a,b$はともに正、示せ
(2)
$b \gt 1$のとき、$a$偶数
(3)
$(a,b)$すべて求めよ
出典:2018年東北大学 過去問
$3^a-2^n=1$ $a,b \varepsilon Z$
(1)
$a,b$はともに正、示せ
(2)
$b \gt 1$のとき、$a$偶数
(3)
$(a,b)$すべて求めよ
出典:2018年東北大学 過去問
単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3^a-2^n=1$ $a,b \varepsilon Z$
(1)
$a,b$はともに正、示せ
(2)
$b \gt 1$のとき、$a$偶数
(3)
$(a,b)$すべて求めよ
出典:2018年東北大学 過去問
$3^a-2^n=1$ $a,b \varepsilon Z$
(1)
$a,b$はともに正、示せ
(2)
$b \gt 1$のとき、$a$偶数
(3)
$(a,b)$すべて求めよ
出典:2018年東北大学 過去問
投稿日:2019.08.29