約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
整数問題 城北高校
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
20以下の自然数nのうち
$(n+1)^2+(n+3)^2+(n+5)^2$が7の倍数となるものは何個？
城北高等学校
この動画を見る
20以下の自然数nのうち
$(n+1)^2+(n+3)^2+(n+5)^2$が7の倍数となるものは何個？
城北高等学校
整数問題 修道高校
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
n(n+1)が88の倍数になるような正の整数nのうち最小のものは？
修道高等学校
この動画を見る
n(n+1)が88の倍数になるような正の整数nのうち最小のものは？
修道高等学校
【高校数学】整数の性質 方程式の問題ではこうやって範囲を絞り込もう！
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
方程式$xy+yz+zx=xyz$を満たす自然数
$x,y,z$の組をすべて求めよ。
この動画を見る
方程式$xy+yz+zx=xyz$を満たす自然数
$x,y,z$の組をすべて求めよ。
【高校数学】整数の性質 約数の総和に関する問題はこうやって解く！
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$N=p^2q$($p,q$は異なる素数)と表される数で
約数の総和が$2N$に等しいものをすべて求めよ。
この動画を見る
$N=p^2q$($p,q$は異なる素数)と表される数で
約数の総和が$2N$に等しいものをすべて求めよ。
整数問題
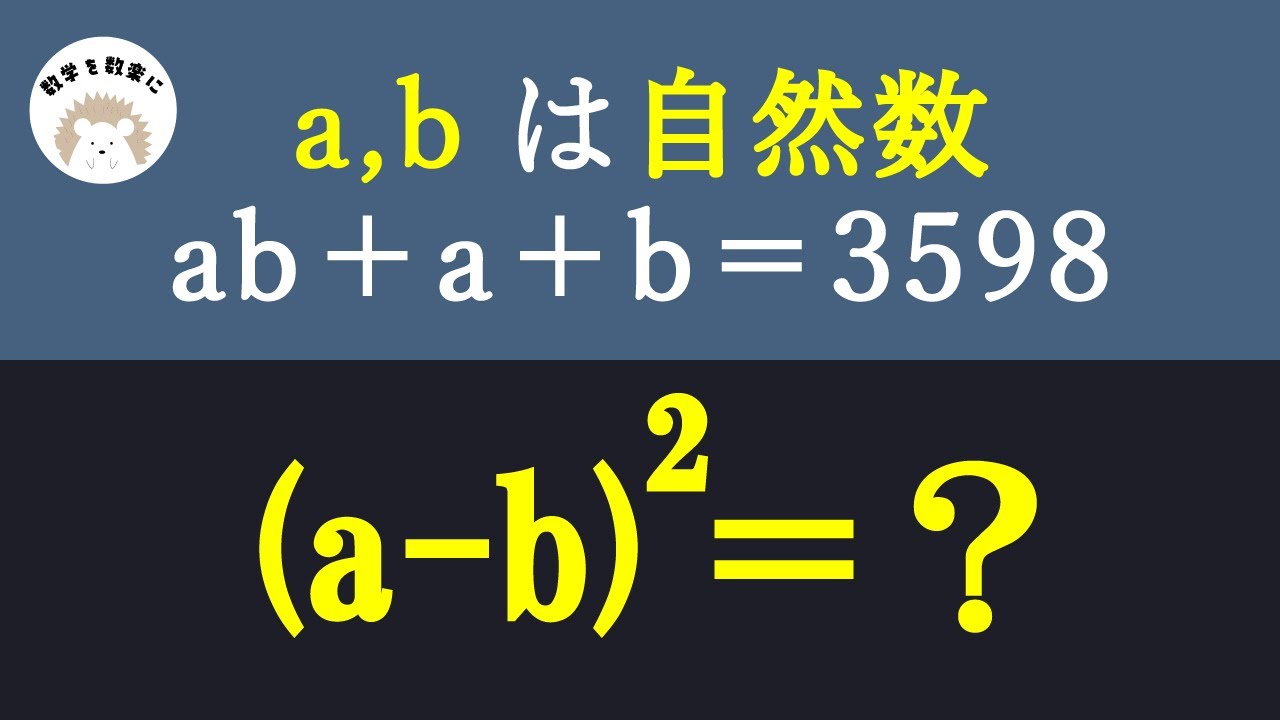
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a,bは自然数
ab+a+b=3598
$(a-b)^2=?$
この動画を見る
a,bは自然数
ab+a+b=3598
$(a-b)^2=?$
約数の個数とその総和 2024明大中野
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
・正の約数を3個だけ持つ
・その約数の総和は871
この自然数を求めよ。
2024明治大学付属中野高等学校
この動画を見る
・正の約数を3個だけ持つ
・その約数の総和は871
この自然数を求めよ。
2024明治大学付属中野高等学校
2024山口大 １の10乗根のナイスな問題
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形と計量#三角比への応用（正弦・余弦・面積）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2Z^4+(1-\sqrt{ 5 })Z^2+2=0$であるとき
(1)$Z^{10}=1$であることを示せ
(2)$\cos \displaystyle \frac{\pi}{5} \cos \displaystyle \frac{2\pi}{5}=\displaystyle \frac{1}{4}$を示せ
出典：2024年山口大学数学 過去問
この動画を見る
$2Z^4+(1-\sqrt{ 5 })Z^2+2=0$であるとき
(1)$Z^{10}=1$であることを示せ
(2)$\cos \displaystyle \frac{\pi}{5} \cos \displaystyle \frac{2\pi}{5}=\displaystyle \frac{1}{4}$を示せ
出典：2024年山口大学数学 過去問
一橋の問題をちょっと変えてみた
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$m,n$正の整数
$100m^2-49n^2=20!$を満たす$(m,n)$の組は何組？
この動画を見る
$m,n$正の整数
$100m^2-49n^2=20!$を満たす$(m,n)$の組は何組？
2024一橋大後期数学 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$m,n$正の整数
$m^2-n^2=10!$を満たす$(m,n)$の組は何組？
出典：2024年一橋大学後期数学 過去問
この動画を見る
$m,n$正の整数
$m^2-n^2=10!$を満たす$(m,n)$の組は何組？
出典：2024年一橋大学後期数学 過去問
2024 慶應女子最初の一問 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$a^2+b^2-2a-4b=20$を満たす
自然数(a,b)の組をすべて求めよ
2024慶應義塾女子高等学校
この動画を見る
$a^2+b^2-2a-4b=20$を満たす
自然数(a,b)の組をすべて求めよ
2024慶應義塾女子高等学校
福田の数学〜慶應義塾大学2024年理工学部第1問(1)〜6番目に大きい約数と6乗根に最も近い自然数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$(1)2024の約数の中で1番大きいものは2024だが,6番目に大きいものは$\boxed{ア}$である.
2024の6乗根に最も近い自然数は$\boxed{イ}$である.
2024慶應義塾大学理工過去問
この動画を見る
$\boxed{1}$(1)2024の約数の中で1番大きいものは2024だが,6番目に大きいものは$\boxed{ア}$である.
2024の6乗根に最も近い自然数は$\boxed{イ}$である.
2024慶應義塾大学理工過去問
福田のおもしろ数学055〜自然数を連続整数の和で表す方法〜偶奇性に注目しよう
福田の数学〜慶應義塾大学2024年理工学部第1問(1)〜6番目に大きい約数と6乗根に最も近い自然数
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
この動画を見る
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
整数の問題& 場合の数 2024早稲田実業
単元：
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
1⃣2⃣3⃣4⃣の4枚のカードを
$▢^▢×▢▢$のように並べる
式の値が3の倍数となる並べ方は何通り？
2024早稲田実業学校
この動画を見る
1⃣2⃣3⃣4⃣の4枚のカードを
$▢^▢×▢▢$のように並べる
式の値が3の倍数となる並べ方は何通り？
2024早稲田実業学校
福田のおもしろ数学052〜余りの問題はこれができなきゃダメ〜余りを求める
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1111^{ 2018 }$ を 11111 で割った余りを求めてください。
この動画を見る
$1111^{ 2018 }$ を 11111 で割った余りを求めてください。
整数部分 2024灘高校の最初の1問
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt {15} + \sqrt{10} $の整数部分は?
灘高等学校2024
この動画を見る
$\sqrt {15} + \sqrt{10} $の整数部分は?
灘高等学校2024
福田のおもしろ数学047〜これができたら天才〜ガウス記号のついた数の和
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$[\dfrac{13×1}{2024}]+[\dfrac{13×2}{2024}]+[\dfrac{13×3}{2024}]+・・・+[\dfrac{13×2023}{2024}]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
この動画を見る
$[\dfrac{13×1}{2024}]+[\dfrac{13×2}{2024}]+[\dfrac{13×3}{2024}]+・・・+[\dfrac{13×2023}{2024}]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
整数問題 2024福岡大附属大濠
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
x-1が9の倍数であるとき$x^2$を3で割った余りは？
2024福岡大学附属大濠高等学校
この動画を見る
x-1が9の倍数であるとき$x^2$を3で割った余りは？
2024福岡大学附属大濠高等学校
福田のおもしろ数学039〜中学生でも理解できる〜素数がむすうに存在する証明その2フェルマー数
福田のおもしろ数学038〜中学生でも理解できる〜素数がむすうに存在する証明その1
7で割ったときのあまりを表せ。宮城県
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
aを29から34までの整数とする。
これを7で割ったときの余りをaの式で表せ。
宮城県
この動画を見る
aを29から34までの整数とする。
これを7で割ったときの余りをaの式で表せ。
宮城県
整数問題 昭和学院秀英
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
n+7が11の倍数でn+11が7の倍数となる正の整数nの中で最小となるnの値を求めよ。
2024昭和学院秀英高等学校
この動画を見る
n+7が11の倍数でn+11が7の倍数となる正の整数nの中で最小となるnの値を求めよ。
2024昭和学院秀英高等学校
11の倍数
整数問題だよ
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n^2+n+144$の下2桁が○○となる3桁の自然数nの最小値と最大値を求めよ.
この動画を見る
$n^2+n+144$の下2桁が○○となる3桁の自然数nの最小値と最大値を求めよ.
福田のおもしろ数学013〜ジュニア数学オリンピックから〜条件を満たす6個の変数は
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c,d,e,f$は相異なる1以上9以下の整数
$ab=cd=e+f$のとき、
$a+b+c+d+e+f$
として考えられる値をすべて求めよ
ジュニア数学オリンピック過去問
この動画を見る
$a,b,c,d,e,f$は相異なる1以上9以下の整数
$ab=cd=e+f$のとき、
$a+b+c+d+e+f$
として考えられる値をすべて求めよ
ジュニア数学オリンピック過去問
福田のおもしろ数学011〜あけましておめでとうございます〜2024の階乗は末尾に0が何個並ぶか
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
2024 !の末尾に並ぶ 0 の個数を求めよ。
この動画を見る
2024 !の末尾に並ぶ 0 の個数を求めよ。
福田のおもしろ数学010〜10秒で解けるキミは天才〜階乗の和の1の位
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
1 !十 2 !十 3 !十・・・十 2023 !十 2024 !の 1 の位を求めよ。
この動画を見る
1 !十 2 !十 3 !十・・・十 2023 !十 2024 !の 1 の位を求めよ。
整数問題 大阪府
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
・2020-nの値は93の倍数
・n-780の値は素数
自然数n=?
2020大阪府
この動画を見る
・2020-nの値は93の倍数
・n-780の値は素数
自然数n=?
2020大阪府
整数問題 戸山高校
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
nは素数
$\frac{100}{n+3}$が整数となるnの値をすべて求めよ。
戸山高等学校
この動画を見る
nは素数
$\frac{100}{n+3}$が整数となるnの値をすべて求めよ。
戸山高等学校
ウィルソンの定理
