単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
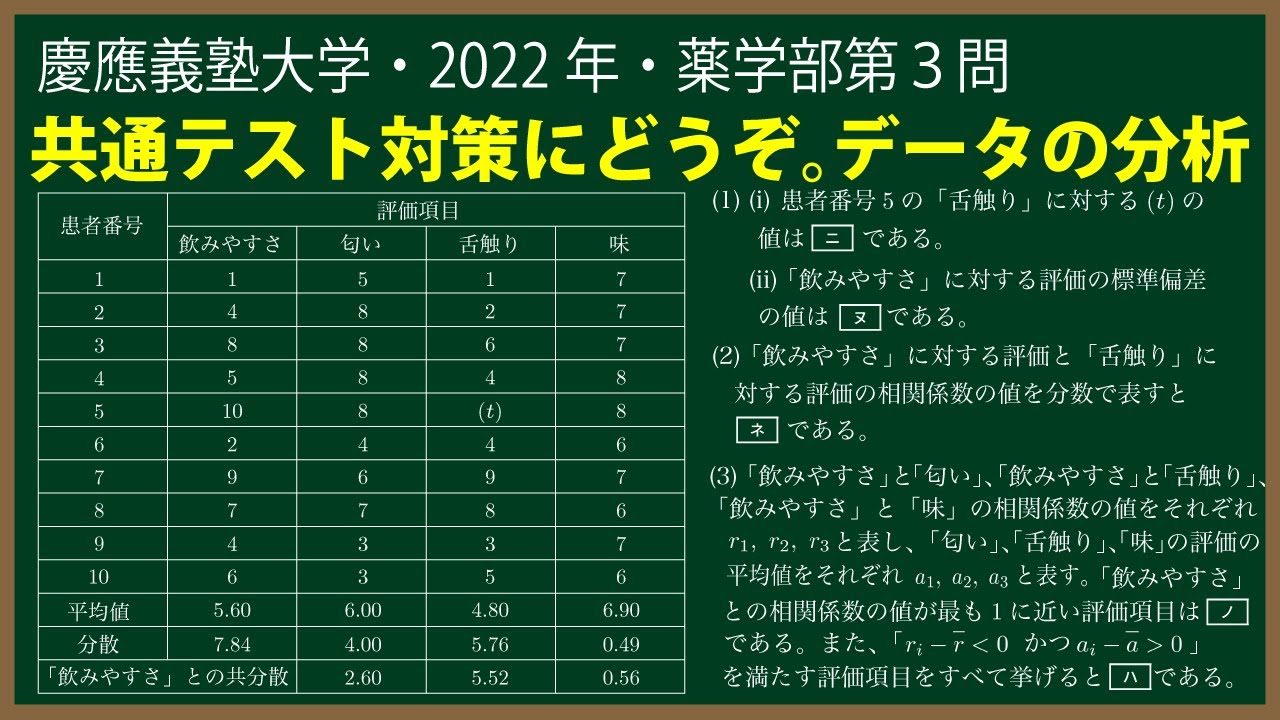
ある病院の入院患者10人に対して、病院内で作っている粉薬の評価を調査した。
調査の評価項目は、粉薬の「飲みやすさ」と、「飲みやすさ」の要因と考えられる
「匂い」「舌触り」、「味」の計4項目についてである。
10人の患者が、評価項目について最も満足な場合は10、最も不安な場合は1として、
1以上10以下の整数で評価した。表内の平均値、分散、共分散の数値は四捨五入
されていない正確な値である。(※動画参照)
「飲みやすさ」との共分散は、「飲みやすさ」に対する評価の偏差と、各評価項目
に対する評価の偏差の積の平均値である。
(1)$(\textrm{i})$患者番号5の「舌触り」に対する(t)の値は$\boxed{\ \ ニ\ \ }$である。
$(\textrm{ii})$「飲みやすさ」に対する評価の標準偏差の値は$\boxed{\ \ ヌ\ \ }$である。
(2)「飲みやすさ」に対する評価と「舌触り」に対する評価の相関係数の値を
分数で表すと$\boxed{\ \ ネ\ \ }$である。
(3)「飲みやすさ」と「匂い」、「飲みやすさ」と「舌触り」、「飲みやすさ」と「味」
の相関係数の値をそれぞれ$r_1,r_2,r_3$と表し、「匂い」、「舌触り」、「味」の評価の
平均値をそれぞれ$a_1,a_2,a_3$と表す。$a_i,r_i (1 \leqq i \leqq 3)$に対し、$\bar{ r }$と$\bar{ a }$は以下の式で定める。
$\bar{ r }=\frac{r_1+r_2+r_3}{3},\bar{ a }=\frac{a_1+a_2+a_3}{3}$
「飲みやすさ」との相関係数の値が最も1に近い評価項目は$\boxed{\ \ ノ\ \ }$である。
また、「$r_i-\bar{ r } \lt0$かつ$a_i-\bar{ a } \gt0$」を満たす評価項目をすべて挙げると$\boxed{\ \ ノ\ \ }$である。
(4)「匂い」、「舌触り」、「味」のうち、$\boxed{\ \ ハ\ \ }$にあてはまらない評価項目
(以降、この評価項目をXと表す)に関して改良を行った。改良後の紛薬に対して、同じ10人の
患者がXと「飲みやすさ」について再び評価した。
改良後の調査結果では、Xの評価は10人全員の評価が改良前に比べてそれぞれ1上がっていた。
改良後のXの評価の平均値を求めると$\boxed{\ \ ヒ\ \ }$であり、標準偏差は改良前調査における値と
比べて$\boxed{\ \ フ\ \ }$。また、「飲みやすさ」の評価については、改良前の調査において評価が
1以上4以下の場合は2上がり、5以上9以下の場合は1上がり、10の場合は評価が変わらず
10であった。よって改良後の「飲みやすさ」に対する評価の平均値を求めると$\boxed{\ \ ヘ\ \ }$であり、
標準偏差は改良前の調査における値と比べて$\boxed{\ \ ホ\ \ }$。
2022慶應義塾大学薬学部過去問
この動画を見る