 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
この手があったか!分母の有理化

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{21}{\sqrt 7}=$
この動画を見る
$\frac{21}{\sqrt 7}=$
これ全部わかる?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$1^0$
②$\sqrt[ 3 ]{ 27 }$
③$2^2$
④$7-1$
⑤$\sqrt{ 49 }$
⑥$2^3$
⑦$\sqrt{ 81 }$
⑧$5+5$
⑨$\sqrt{ 144 }$
この動画を見る
①$1^0$
②$\sqrt[ 3 ]{ 27 }$
③$2^2$
④$7-1$
⑤$\sqrt{ 49 }$
⑥$2^3$
⑦$\sqrt{ 81 }$
⑧$5+5$
⑨$\sqrt{ 144 }$
数と式 4S数学問題集数Ⅰ 60,61平方根の近似値【さこすけ’s サイエンスがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{2}=1.4142$, $\sqrt{3}=1.7321$
とするとき, 分母の有理化を利用して, 次の値を求めよ。
(1) $\dfrac{10}{\sqrt{3}+\sqrt{2}}$ (2) $\dfrac{1}{\sqrt{12}-\sqrt{2}}$
$x=1-\sqrt{5}$
のとき, 次の式の値を求めよ。
(1) $x^2-2x-4$ (2) $x^3-2x^2$
この動画を見る
$\sqrt{2}=1.4142$, $\sqrt{3}=1.7321$
とするとき, 分母の有理化を利用して, 次の値を求めよ。
(1) $\dfrac{10}{\sqrt{3}+\sqrt{2}}$ (2) $\dfrac{1}{\sqrt{12}-\sqrt{2}}$
$x=1-\sqrt{5}$
のとき, 次の式の値を求めよ。
(1) $x^2-2x-4$ (2) $x^3-2x^2$
数と式 4S数学問題集数Ⅰ 58,59 平方根の式の値【さこすけ’s サイエンスがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x=\dfrac{\sqrt{ 5 }+2}{\sqrt{ 5 }-2}$ , $y=\dfrac{\sqrt{ 5 }-2}{\sqrt{ 5 }+2}$
のとき, 次の式の値を求めよ。
(1) $x+y$ (2) $xy$ (3) $x^2y+xy^2 $
(4) $x^2+y^2$ (5) $x^3+y^3$
$x=\sqrt{ 2 }-1$
のとき, 次の式の値を求めよ。
(1) $x+\dfrac{1}{x}$ (2) $x^2+\dfrac{1}{x^2}$ (3) $x^3+\dfrac{1}{x^3}$
(4) $x^4+\dfrac{1}{x^4}$ (5) $x^5+\dfrac{1}{x^5}$
この動画を見る
$x=\dfrac{\sqrt{ 5 }+2}{\sqrt{ 5 }-2}$ , $y=\dfrac{\sqrt{ 5 }-2}{\sqrt{ 5 }+2}$
のとき, 次の式の値を求めよ。
(1) $x+y$ (2) $xy$ (3) $x^2y+xy^2 $
(4) $x^2+y^2$ (5) $x^3+y^3$
$x=\sqrt{ 2 }-1$
のとき, 次の式の値を求めよ。
(1) $x+\dfrac{1}{x}$ (2) $x^2+\dfrac{1}{x^2}$ (3) $x^3+\dfrac{1}{x^3}$
(4) $x^4+\dfrac{1}{x^4}$ (5) $x^5+\dfrac{1}{x^5}$
【短時間でポイントチェック!!】絶対値を含む定積分〔現役講師解説、数学〕

単元:
#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\int_1^3{|x^2-4|}dx$
この動画を見る
$\int_1^3{|x^2-4|}dx$
福田のおもしろ数学049〜1分チャレンジ〜5重根号に挑戦!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{ 2024\sqrt{ 2023\sqrt{ 2022\sqrt{ 2021\sqrt{ 2020×2018+1 }+1 }+1 }+1 }+1}$を計算してください。
この動画を見る
$\sqrt{ 2024\sqrt{ 2023\sqrt{ 2022\sqrt{ 2021\sqrt{ 2020×2018+1 }+1 }+1 }+1 }+1}$を計算してください。
2024年共通テスト速報〜数学ⅠA第1問の(1)〜福田の入試解説

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
この動画を見る
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
【ひらめきに頼らず…!】整数:灘高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \color{orange}{x^2+x-n+1=0}$が整数解をもつような$ \color{red}{整数n}$のうち
$ \color{red}{n-2023の絶対値}$が最も小さいものは$ \Box $である.
$ \Box $を解け.
灘高校過去問
この動画を見る
$ \color{orange}{x^2+x-n+1=0}$が整数解をもつような$ \color{red}{整数n}$のうち
$ \color{red}{n-2023の絶対値}$が最も小さいものは$ \Box $である.
$ \Box $を解け.
灘高校過去問
ミスリードに気をつけろ!久留米大(医)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\displaystyle \frac{3}{2\sqrt13-7}$
整数部分と小数部分を求めよ
(2)$\displaystyle \frac{2}{a-\sqrt7}$
整数部分が5である。整数aを求めよ
この動画を見る
(1)$\displaystyle \frac{3}{2\sqrt13-7}$
整数部分と小数部分を求めよ
(2)$\displaystyle \frac{2}{a-\sqrt7}$
整数部分が5である。整数aを求めよ
数と式 4S数学問題集数Ⅰ 56,57,58 平方根の計算【さこすけ’s サイエンスがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
56 次の計算をせよ。
(1) $(1+\sqrt{ 2 }-\sqrt{ 3 })^2$
(2)$(3-\sqrt{ 2 }-\sqrt{ 11 })(3-\sqrt{ 2 }+\sqrt{ 11 })$
57 次の計算をせよ。
(1) $\displaystyle \frac{3\sqrt{ 5 }-5\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}+\displaystyle \frac{3\sqrt{ 5 }+4\sqrt{ 3 }}{3\sqrt{ 5 }-4\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 2 }-1}{\sqrt{ 2 }+1}+\displaystyle \frac{\sqrt{ 3 }-\sqrt{ 2 }}{\sqrt{ 3 }+\sqrt{ 2 }}+\displaystyle \frac{\sqrt{ 3 }+\sqrt{ 2 }}{2-\sqrt{ 3 }}$
63 次の計算をせよ。
(1) $\displaystyle \frac{1}{1+\sqrt{ 2 }-\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }+\sqrt{ 2 }}{\sqrt{ 5 }+\sqrt{ 3 }-\sqrt{ 2 }}$
(3) $\displaystyle \frac{\sqrt{ 2 }+\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }+\sqrt{ 5 }-\sqrt{ 7 }}+\displaystyle \frac{\sqrt{ 2 }-\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }-\sqrt{ 5 }-\sqrt{ 7 }}$
この動画を見る
56 次の計算をせよ。
(1) $(1+\sqrt{ 2 }-\sqrt{ 3 })^2$
(2)$(3-\sqrt{ 2 }-\sqrt{ 11 })(3-\sqrt{ 2 }+\sqrt{ 11 })$
57 次の計算をせよ。
(1) $\displaystyle \frac{3\sqrt{ 5 }-5\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}+\displaystyle \frac{3\sqrt{ 5 }+4\sqrt{ 3 }}{3\sqrt{ 5 }-4\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 2 }-1}{\sqrt{ 2 }+1}+\displaystyle \frac{\sqrt{ 3 }-\sqrt{ 2 }}{\sqrt{ 3 }+\sqrt{ 2 }}+\displaystyle \frac{\sqrt{ 3 }+\sqrt{ 2 }}{2-\sqrt{ 3 }}$
63 次の計算をせよ。
(1) $\displaystyle \frac{1}{1+\sqrt{ 2 }-\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }+\sqrt{ 2 }}{\sqrt{ 5 }+\sqrt{ 3 }-\sqrt{ 2 }}$
(3) $\displaystyle \frac{\sqrt{ 2 }+\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }+\sqrt{ 5 }-\sqrt{ 7 }}+\displaystyle \frac{\sqrt{ 2 }-\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }-\sqrt{ 5 }-\sqrt{ 7 }}$
数と式 4S数学問題集数Ⅰ 50,51 循環小数と絶対値【さこすけ’s サイエンスがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
50 次の分数を小数で表したとき、[ ]内の数字を求めよ。
(1) $\frac{11}{101}$ (2) $\frac{9}{41}$
51 x=-4,-1,2,5 のそれぞれについて、次の式の値を求めよ。
(1)|-x| (2)|x+1| (3)|1-2x|+|x-1|
この動画を見る
50 次の分数を小数で表したとき、[ ]内の数字を求めよ。
(1) $\frac{11}{101}$ (2) $\frac{9}{41}$
51 x=-4,-1,2,5 のそれぞれについて、次の式の値を求めよ。
(1)|-x| (2)|x+1| (3)|1-2x|+|x-1|
佐賀大(医)無理数の証明

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2018年 佐賀大学医学部 過去問
①nが平方数でない自然数のとき、
$\sqrt{n}$は無理数であることを示せ。
②$a,b$は正の有理数、$m$は自然数のとき、
$a\sqrt{m}+b\sqrt{m + 1}$
は無理数であることを示せ。
この動画を見る
2018年 佐賀大学医学部 過去問
①nが平方数でない自然数のとき、
$\sqrt{n}$は無理数であることを示せ。
②$a,b$は正の有理数、$m$は自然数のとき、
$a\sqrt{m}+b\sqrt{m + 1}$
は無理数であることを示せ。
ほぼ自明な証明ほど難しい?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{2}+\sqrt{3}$
が無理数であることを証明せよ。
この動画を見る
$\sqrt{2}+\sqrt{3}$
が無理数であることを証明せよ。
3乗根が綺麗になっちゃった

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a≧\frac{1}{8}$
$\sqrt[3]{a+\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}+\sqrt[3]{a-\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}$
この動画を見る
$a≧\frac{1}{8}$
$\sqrt[3]{a+\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}+\sqrt[3]{a-\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}$
【ホーン・フィールドがていねいに解説】数と式 4S数学問題集数Ⅰ 62,64 根号を含む計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
√2/(√2-1)の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)a (2)b (3)a+b+b²
次の各場合について、√(x²-10x+25)をxの多項式で表せ。
(1)x≧5 (2)x<5
この動画を見る
√2/(√2-1)の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)a (2)b (3)a+b+b²
次の各場合について、√(x²-10x+25)をxの多項式で表せ。
(1)x≧5 (2)x<5
【高校数学】気持ちいい計算問題!ずばずば消えて残るのはたったのこれだけ!? #Shorts

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\displaystyle \frac{\sqrt{2}-\sqrt{1}}{\sqrt[4]{2}+\sqrt[4]{1}}$+$\displaystyle \frac{\sqrt{3}-\sqrt{2}}{\sqrt[4]{3}+\sqrt[4]{2}}$+・・・・・・+$\displaystyle \frac{\sqrt{20}-\sqrt{19}}{\sqrt[4]{20}+\sqrt[4]{19}}$
気持ちよい計算問題です。
この動画を見る
$\displaystyle \frac{\sqrt{2}-\sqrt{1}}{\sqrt[4]{2}+\sqrt[4]{1}}$+$\displaystyle \frac{\sqrt{3}-\sqrt{2}}{\sqrt[4]{3}+\sqrt[4]{2}}$+・・・・・・+$\displaystyle \frac{\sqrt{20}-\sqrt{19}}{\sqrt[4]{20}+\sqrt[4]{19}}$
気持ちよい計算問題です。
【数検準2級】高校数学:数学検定準2級2次:問2

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問2.次の問いに答えなさい。
(3) 正の数xに対して、xを超えない最大の整数をxの整数部分、xからxの整数部分を引いた値をxの小数部分といいます。
たとえば√2(=1.414…)については、1<√2<2より、√2の整数部分は1、√2の小数部分は√2-1となります。
√5の小数部分をaとするとき、a²+4aの値を求めなさい。
この動画を見る
問2.次の問いに答えなさい。
(3) 正の数xに対して、xを超えない最大の整数をxの整数部分、xからxの整数部分を引いた値をxの小数部分といいます。
たとえば√2(=1.414…)については、1<√2<2より、√2の整数部分は1、√2の小数部分は√2-1となります。
√5の小数部分をaとするとき、a²+4aの値を求めなさい。
場合分けは何パターン?多くの絶対値を含んだ問題【京都大学】【数学 入試問題】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$が整数であるとき$S=\vert n-1 \vert+\vert n-2 \vert+……+\vert n-100 \vert$の最小値を求めよ。
また、そのときの$n$の値を求めよ。
この動画を見る
$n$が整数であるとき$S=\vert n-1 \vert+\vert n-2 \vert+……+\vert n-100 \vert$の最小値を求めよ。
また、そのときの$n$の値を求めよ。
2023早稲田(社)三乗根の計算

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}とする.
(1)a^3をaの一次式で表せ.
(2)aは整数であることを示せ.
(3)b=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}とするとき,bを越えない最大の整数を求めよ.$
この動画を見る
$a=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}とする.
(1)a^3をaの一次式で表せ.
(2)aは整数であることを示せ.
(3)b=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}とするとき,bを越えない最大の整数を求めよ.$
【短時間でマスター!!】整数(平方根が自然数になる問題)を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
整数
$\sqrt{600n}$が自然数となるような最小の自然数$n$は?
$\sqrt{\frac{72}{n}}$が自然数となるような最小の自然数$n$は?
この動画を見る
数学1A
整数
$\sqrt{600n}$が自然数となるような最小の自然数$n$は?
$\sqrt{\frac{72}{n}}$が自然数となるような最小の自然数$n$は?
2023京都大学 3乗根の分母の有理化

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$分母を有利化せよ.
\dfrac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
この動画を見る
$分母を有利化せよ.
\dfrac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
数1の基本問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x+(2a^2-a+6)・2^x+2a^2+a-6=0が実数解をもつaの範囲を求めよ.$
この動画を見る
$4^x+(2a^2-a+6)・2^x+2a^2+a-6=0が実数解をもつaの範囲を求めよ.$
根号を外すだけの問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$いくつですか?
\sqrt{55×56×57+1}$
この動画を見る
$いくつですか?
\sqrt{55×56×57+1}$
【数学】有理化がなぜ必要なのか?解説してみた!

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
有理化って何のためにしてるか知っていますか??
この動画を見る
有理化って何のためにしてるか知っていますか??
出題者の意図を汲みとるだけの問題。灘高の計算

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ ①(2\sqrt2-3)^2=?,
②\sqrt{\sqrt{(10-7\sqrt2}^2)-\sqrt{(7-5\sqrt2}^2)}=?
?を求めよ.$
この動画を見る
$ ①(2\sqrt2-3)^2=?,
②\sqrt{\sqrt{(10-7\sqrt2}^2)-\sqrt{(7-5\sqrt2}^2)}=?
?を求めよ.$
ナイスな連立方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ これを解け.x,yを正の実数とする.
\begin{eqnarray}
\left\{
\begin{array}{l}
x\sqrt x+y\sqrt y=32 \\
x\sqrt y+y\sqrt x=31
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$ これを解け.x,yを正の実数とする.
\begin{eqnarray}
\left\{
\begin{array}{l}
x\sqrt x+y\sqrt y=32 \\
x\sqrt y+y\sqrt x=31
\end{array}
\right.
\end{eqnarray}$
二重根号の整数問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{n+\sqrt{n+7}}が整数となる自然数nをすべて求めよ.$
この動画を見る
$ \sqrt{n+\sqrt{n+7}}が整数となる自然数nをすべて求めよ.$
解けるように作られた根号方程式
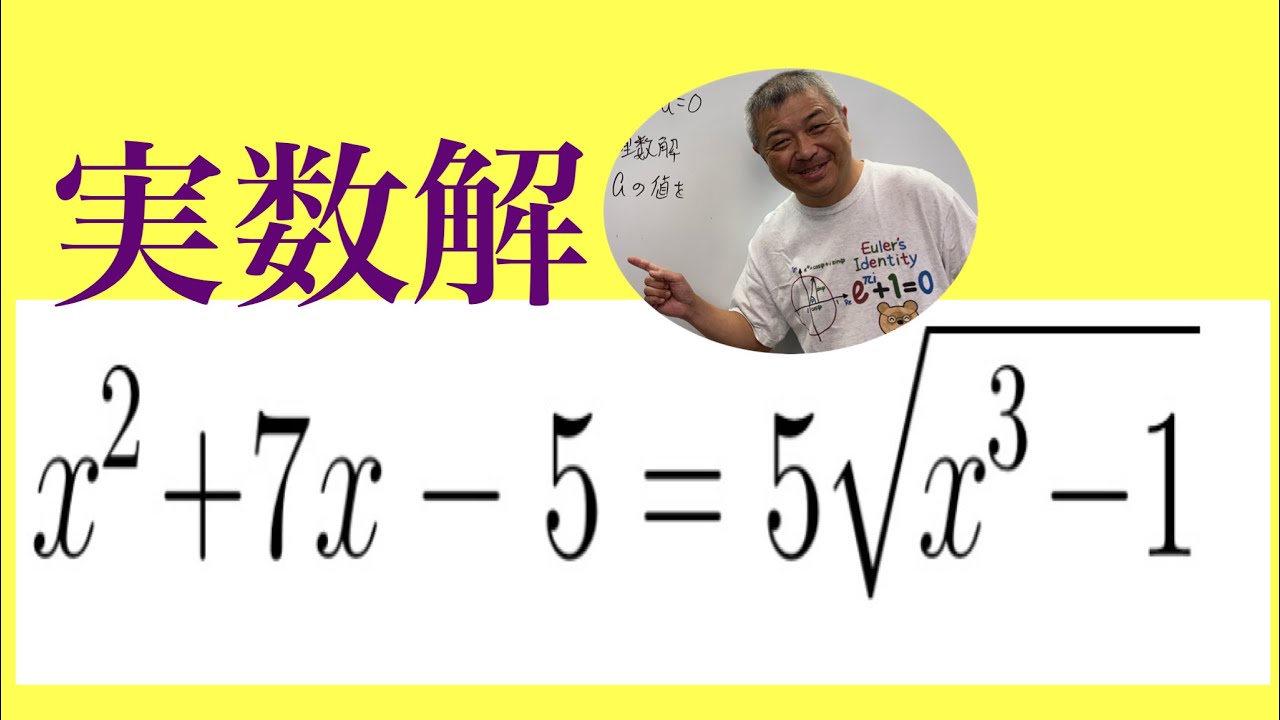
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+7x-5=5\sqrt{x^3-1},これの実数解を求めよ.$
この動画を見る
$ x^2+7x-5=5\sqrt{x^3-1},これの実数解を求めよ.$
平方根の方程式 あれに気をつけて

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{6x+7}-\sqrt{9x+1}=1,これを解け.$
この動画を見る
$ \sqrt{6x+7}-\sqrt{9x+1}=1,これを解け.$
あれのオンパレード!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{\dfrac{99^4+101^4+200^4}{2}},これを解け.$
この動画を見る
$ \sqrt{\dfrac{99^4+101^4+200^4}{2}},これを解け.$
